Een regelmatig veelvlak is een veelvlak met volgende eigenschappen:

• Alle zijvlakken zijn congruente regelmatige veelhoeken.
• In elk hoekpunt komen evenveel zijvlakken samen.
• Ze zijn convex
• De hoeken tussen de zijvlakken zijn steeds hetzelfde.
• Voor het aantal ribben (R), het aantal grensvlakken (G) en aantal hoekpunten (H) van een convex lichaam geldt de formule van Euler: R + 2 = G + H

Er zijn er 5; ze worden ook wel eens de Platonische lichamen genoemd naar Plato(427 BC – 347BC), die ze het eerst beschreef.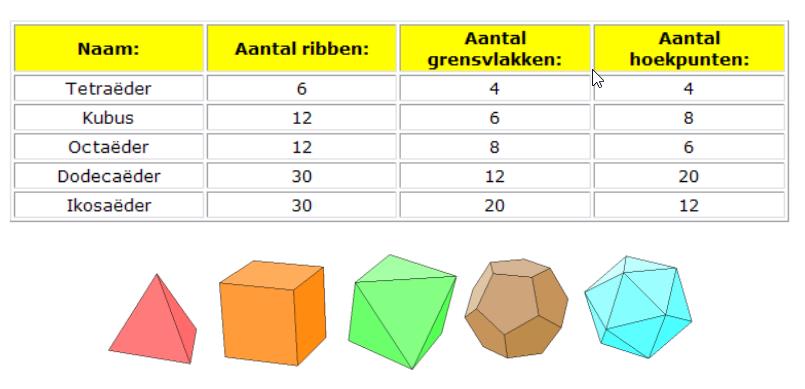

Plato bracht de vijf regelmatige veelvlakken ook in verband met de vijf kosmische bouwstenen van de wereld: vuur, lucht, water, aarde en hemelmaterie.

Verbindt men de middens van de zijvlakken van een veelvlak met elkaar, dan vormen de verbindingslijnen de ribben van een ander veelvlak. Een viervlak blijft een viervlak, maar een kubus wordt een octaëder en omgekeerd. Een dodecaëder wordt een icosaëder en omgekeerd. De kubus en de octaëder zijn het duale veelvlak van elkaar, de dodecaëder en de icosaëder ook.