Wiskunde is leuk

Opgave 9

Geplaatst op 6 januari 2018 door admin

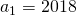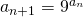Definieer $a_1=2018$ en $a_{n+1}=9^{a_n}$ voor n=1,2,…
Bepaal de laatste twee cijfers van 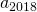$a_{2018}$ .

Antwoord

We kunnen voor 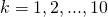$k=1,2,...,10$ de laatste twee cijfers berekenen van 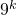$9^k$ . We vinden 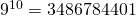$9^{10}=3486784401$ en eindigt dus op $01$ .
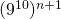Als $(9^{10})^n$ eindigt op 01, dan zal ook $(9^{10})^{n+1}$ eindigen op 01, want $(9^{10})^{n+1}=(9^{10})^n.9^{10}=(\cdots 01).(\cdots 01)=(\cdots 01)$ .
Door inductie hebben we dus bewezen dat elke macht van $9^ {10}$ eindigt op 01.
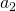Dan is $a_2=9^{2018}=(9^{10})^{201}.9^8=(\cdots01).43046721$ en dus eindigt $a_2$ op 21.
Verder is $a_3=9^{\cdots 21}=(9^{10})^{\cdots 2}.9^1=(\cdots 01).9=\cdots 09$ . Bijgevolg eindigt $a_3$ op 09.
Nu is $a_4=9^{\cdots 09}=(9^{10})^{\cdots 0}.9^9=(\cdots 01).387420489=\cdots 89$ .
Het is duidelijk dat alle verdere termen van de rij op 89 zullen eindigen.
Dus 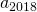$a_{2018}$ eindigt op 89.