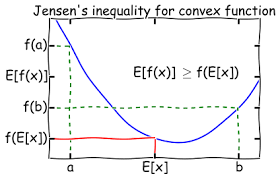
Ongelijkheid van Jensen | Wiskunde is leuk

Voor elke functie f waarvan de grafiek ‘hol’ naar onder is , of dus convex (d.w.z dat het verbindingstuk van twee punten van de grafiek altijd boven de grafiek ligt ) geldt volgende ongelijkheid:

$f(\dfrac{a_1+a_2+\cdots+\a_n}{n} )\leq \dfrac{f(a_1)+f(a_2)+\cdots+f(a_n)}{n}$

Deze ongelijkheid staat bekend als de ongelijkheid van Jensen, naar de Deense wiskundige Johan Willem Ludwig Valdemar Jensen (1859-1925).

Uiteraard is er een analoge formule voor concave functies.

Voorbeeld: Als a,b en c positieve hoeken zijn met een som gelijk aan $\frac{\pi}{2}$ , dan is $\tan a+ \tan b+\tan c \geq \sqrt{3}$ .

Tussen 0 en $\frac{\pi}{2}$ is de tangensfunctie convex, dus geldt er volgens Jensen dat $\tan (\dfrac{a+b+c}{3}) \leq \frac{1}{3}( \tan a+\tan b+\tan c)$ . Hieruit volgt dat $\frac{1}{3}( \tan a+\tan b+\tan c) \geq \tan(\frac{\pi}{6})=\frac{\sqrt{3}}{3}$ . Vermenigvuldigen met 3 geeft het gevraagde antwoord.