Nootje 31

Geplaatst op door

Gegeven is A=\begin{pmatrix} \cos x&-\sin x\\ \sin x &\cos x \end{pmatrix}. Bereken A^{-50} voor x=15^{\circ}.

Antwoord

  • Het zal zeker niet de bedoeling zijn om deze macht uit te rekenen.
  • Matrix A is eigenlijk de matrix voorstelling van het complex getal

        \[\cos x + i \sin x\]

  • Gebruik van de formule van Lemoivre geeft

        \[A^{-50}=\begin{pmatrix} \cos -50x&-\sin -50x\\ \sin -50x &\cos -50x \end{pmatrix}\]

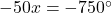  • Nu is -50x=-750^{\circ}. We mogen altijd een veelvoud van 360^{\circ} bijvoegen zodat: 

        \[A^{-50}=\begin{pmatrix} \cos -30^{\circ}&-\sin -30^{\circ}\\ \sin -30^{\circ} &\cos -30^{\circ} \end{pmatrix}\]

  • Uitrekenen geeft

        \[A^{-50}=\frac{1}{2}\begin{pmatrix} \sqrt{3}&1\\-1&\sqrt{3}\end{pmatrix}\]