Om te bewijzen dat ![]() aftelbaar oneindig is, moeten we een bijectie opstellen tussen
aftelbaar oneindig is, moeten we een bijectie opstellen tussen ![]() en
en ![]() . We kunnen dit doen via de diagonaalmethode van Cantor :
. We kunnen dit doen via de diagonaalmethode van Cantor :
De volgende tekening spreekt voor zich: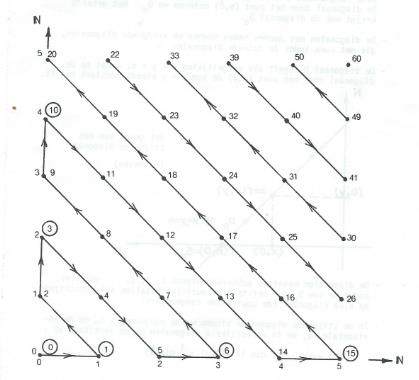
Met volgende formule kan je het rangnummer bepalen van een bepaald punt ![]() :
:
![]()
Het is wel moeilijker om met één natuurlijk getal z een koppel natuurlijke getallen te laten overeenkomen.
- De diagonalen bevatten achtereenvolgens 1,2,3,… getallen, zodat de som
 van de eerste n natuurlijke getallen zal verschijnen op elke diagonaal ( de omcirkelde rangnummers) .
van de eerste n natuurlijke getallen zal verschijnen op elke diagonaal ( de omcirkelde rangnummers) . - Aangezien z gelegen is tussen twee opeenvolgende waarden van
 , moet n gelijk zijn aan het aantal gehelen
, moet n gelijk zijn aan het aantal gehelen  van de positieve wortel van de vierkantsvergelijking
van de positieve wortel van de vierkantsvergelijking 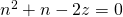 .
. - Als
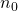 even is, dan behoort
even is, dan behoort 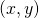 tot een dalende diagonaal en is
tot een dalende diagonaal en is  en
en  .
. - Als
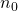 oneven is, dan behoort
oneven is, dan behoort 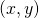 tot een stijgende diagonaal en is
tot een stijgende diagonaal en is 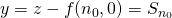 en
en 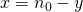 .
.
Neem bijvoorbeeld het getal z met rangnummer 32. De vierkantsvergelijking ![]() heeft bij benadering als oplossingen -8,52 en 7,52. Dus is
heeft bij benadering als oplossingen -8,52 en 7,52. Dus is ![]() . Het corresponderend punt in het vlak is
. Het corresponderend punt in het vlak is ![]() .
.
Neem als tweede voorbeeld het getal z met rangnummer 38. De bijhorende vierkantsvergelijking ![]() heeft bij benadering als oplossingen -9,23 en 8,23 zodat
heeft bij benadering als oplossingen -9,23 en 8,23 zodat ![]() . Het corresponderend punt in het vlak is
. Het corresponderend punt in het vlak is ![]()