De eindige rekenkunde, ook wel modulaire rekenkunde genoemd, wordt beschreven in het boek Disquisitiones Arithmeticae van Gauss, een buitengewoon invloedrijk werk uit 1801, toen de auteur nog maar vierentwintig jaar oud was.
Stel ![]() . Indien
. Indien ![]() en
en ![]() bij deling door
bij deling door ![]() dezelfde rest geven, d.w.z. indien
dezelfde rest geven, d.w.z. indien ![]() voor zekere
voor zekere ![]() , heten
, heten ![]() en
en ![]() congruent modulo
congruent modulo ![]() . We noteren
. We noteren ![]() mod m.Zo is bijvoorbeeld
mod m.Zo is bijvoorbeeld ![]() mod 5,
mod 5, ![]() mod 8 en
mod 8 en ![]() mod 13.
mod 13.
Enkele eigenschappen :
- Als
 mod m en
mod m en  mod m, dan is
mod m, dan is  mod m.
mod m. - Als
 mod m en
mod m en 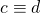 mod m, dan is
mod m, dan is  mod m.
mod m. - Als
 mod m en
mod m en  , dan is
, dan is  mod m.
mod m. - Als
 mod m dan is voor elke
mod m dan is voor elke  :
:  mod m.
mod m. - Als
 mod m en
mod m en 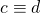 mod m, dan is
mod m, dan is  mod m.
mod m.
Rekenen met congruenties lijkt erg op het rekenen met vergelijkingen. Er is echter een belangrijk verschil: uit ![]() mod m met
mod m met ![]() mod m hoeft niet te volgen dat
mod m hoeft niet te volgen dat ![]() mod m. Zo is
mod m. Zo is ![]() mod 10 maar 12 is niet congruent met 7 modulo 10. In andere gevallen gaat het wel op. De voorwaarde waarop de vereenvoudiging met
mod 10 maar 12 is niet congruent met 7 modulo 10. In andere gevallen gaat het wel op. De voorwaarde waarop de vereenvoudiging met ![]() wel kan, is dat
wel kan, is dat ![]() onderling ondeelbaar is met
onderling ondeelbaar is met ![]() .
.
Dus als ![]() mod m en ggd(c,m) = 1, dan is
mod m en ggd(c,m) = 1, dan is ![]() mod m.
mod m.
Als ggd(c,m) = d, dan volgt uit ![]() mod m dat
mod m dat ![]() mod(
mod( ![]() ).
).
Rekent men modulo ![]() , dan zijn er
, dan zijn er ![]() verschillende soorten getallen, al naar gelang ze verschillende resten geven bij deling door
verschillende soorten getallen, al naar gelang ze verschillende resten geven bij deling door ![]() . De verzameling van alle gehele getallen die eenzelfde rest geven heet een restklasse modulo
. De verzameling van alle gehele getallen die eenzelfde rest geven heet een restklasse modulo ![]() . Er zijn dus precies
. Er zijn dus precies ![]() verschillende restklassen modulo
verschillende restklassen modulo ![]() . De restklasse die een getal
. De restklasse die een getal ![]() bevat, noteert men als
bevat, noteert men als ![]() . Deze notatie is natuurlijk niet eenduidig bepaald, want als
. Deze notatie is natuurlijk niet eenduidig bepaald, want als ![]() mod m, stellen
mod m, stellen ![]() en
en ![]() dezelfde restklasse modulo
dezelfde restklasse modulo ![]() voor en omgekeerd.
voor en omgekeerd.
Werken we modulo 4 dan is ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Men kan in de verzameling restklassen modulo ![]() , genoteerd door
, genoteerd door ![]() , een optelling en een vermenigvuldiging defini\”eren via
, een optelling en een vermenigvuldiging defini\”eren via ![]() en
en ![]() . Deze rekenregels lijken erg op de regels van optelling en vermenigvuldiging van gehele getallen.
. Deze rekenregels lijken erg op de regels van optelling en vermenigvuldiging van gehele getallen.
Eigenschappen :

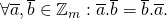
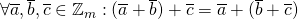 .
. .
. .
.
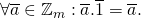
- Er is een unieke restklasse
 met
met  , namelijk
, namelijk  .
.
Veronderstel dat we de rest willen bepalen van ![]() bij deling door 7. Omdat
bij deling door 7. Omdat ![]() mod 7 en
mod 7 en ![]() mod 7, moet
mod 7, moet ![]() mod 7
mod 7 ![]() mod 7
mod 7 ![]() mod 7. Dus de rest bij deling van
mod 7. Dus de rest bij deling van ![]() door 7 is 2. We moeten daarvoor het product niet uitrekenen.
door 7 is 2. We moeten daarvoor het product niet uitrekenen.

