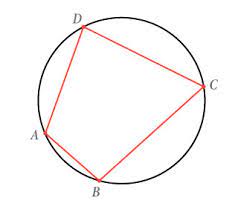
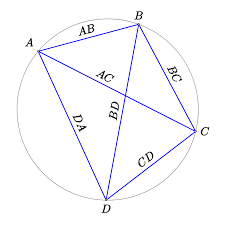
Een koordenvierhoek is een vierhoek waarvan de hoekpunten op een cirkel gelegen zijn. Deze cirkel noemen we dan de omgeschreven cirkel.

Een paar eigenschappen:

• Bij een koordenvierhoek zijn de overstaande hoeken supplementair en omgekeerd, als bij een vierhoek elke twee overstaande hoeken supplementair zijn, dan is die vierhoek een koordenvierhoek. Bijgevolg zijn een vierkant , een rechthoek , een gelijkbenig trapezium  allemaal koordenvierhoeken.
• Van een koordenvierhoek is het product van de diagonalen gelijk aan de som van de producten van de overstaande zijden  en omgekeerd (stelling van Ptolemeus): 
         

     

• De verhouding van de diagonalen van een koordenvierhoek is gelijk aan de verhouding van de sommen van de producten van de zijden, die in hun uiteinden samenkomen: