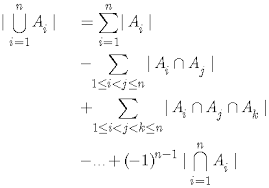Inclusie-exclusiestelling | Wiskunde is leuk

Veronderstel dat $A_i$ eindige deelverzamelingen zijn van U en noteer met $|A_i|$ het aantal elementen van $A_i$ , dan geldt:

We noemen dit de inclusie-exclusie stelling.

Noteer $S_i$ de som van het aantal elementen in alle mogelijke doorsneden van i verzamelingen $A_i$ . Merk op dat $S_i$ precies ${n} \choose {i}$ termen bevat. Noteer met $S_0$ het aantal elementen van U. Formuleren we nu een algemenere versie van vorig resultaat:

Het aantal elementen van U dat tot precies m verzamelingen $A_i$ behoort, wordt gegeven door de formule:

$\sum_{i=0}^{n-m}(-1)^i \binom{m+i} {m} S_{m+i}$

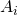Voor $m=n$ vinden we het aantal elementen dat tot alle $A_i$ behoren.
Voor 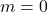$m=0$ vinden we het aantal elementen dat tot geen enkele 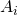$A_i$ behoort.

Vind het aantal getallen tussen 1 en 1000 dat niet deelbaar is door 2,3,5 of 7.
Stem $A_m=\{k\leq 1000 \text{ zodat k een m-voud is }\}$ .
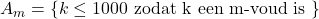Het is eenvoudig na te rekenen dat 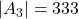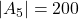$|A_2|=500$ , $|A_3|=333$ , $|A_5|=200$ en $|A_7|=142$ . Bijgevolg is $S_1=1175$ .
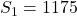Er zijn 166 getallen die een 2 en 3 voud zijn. Er zijn 100 getallen die een veelvoud zijn van 2 en 5. Er zijn 71 getallen die een veelvoud zijn van 2 en 7. Er zijn 66 getallen die een veelvoud zijn van 3 en 5. Er zijn 47 getallen die een veelvoud zijn van 3 en 7. Er zijn 28 getallen die een veelvoud zijn van 5 en 7. Dus is $S_2=478$ .
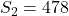Eenvoudig narekenen geeft dat $S_3=79$ .
Er zijn 4 getallen die zowel deelbaar zijn door 2,3,5 en 7. Dus $S_4=4$ .
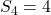Het aantal getallen dat door geen van de cijfers 2,3,5 of 7 deelbaar is, is dan ook gelijk aan: $1000-1175+478-79+4=228$ .
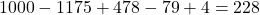Het aantal getallen dat door één van de cijfers deelbaar is, wordt gegeven door : $1*1175-2*478+3*79-4*4=440$ . Voor twee vinden we 265; voor drie 63 en tenslotte voor vier 4.

AI assistent 4.0 geeft een antwoord, maar dat is duidelijk fout!

Er zijn 720 getallen tussen 1 en 1000 die niet deelbaar zijn door 2, 3, 5 of 7. Je kunt dit aantal berekenen door alle cijfers tussen 1 en 1000 te tellen die deelbaar zijn door 2, 3, 5 of 7:

2: 500
3: 333
5: 200
7: 142

Totaal: 1225 getallen

Aantal getallen tussen 1 en 1000 die niet deelbaar zijn door 2, 3, 5 of 7: 1000 – 1225 = 720