In 1907 werd een bundeling van meer dan 100 puzzelproblemen gepubliceerd in het boek Canterbury puzzels van Henry Dudeney (1857 – 1930 . Dudeney was een Engels auteur en wiskundige met een voorliefde voor logische puzzels en wiskundige spelletjes. Eén van de meest bekende puzzels is de volgende: gegeven is een gelijkzijdige driehoek. Maak met slechts 3 insnijdingen van de driehoek 4 puzzelstukjes die kunnen omgevormd worden tot een vierkant met dezelfde oppervlakte als de gegeven driehoek.
Een mogelijke oplossing wordt gegeven als volgt:
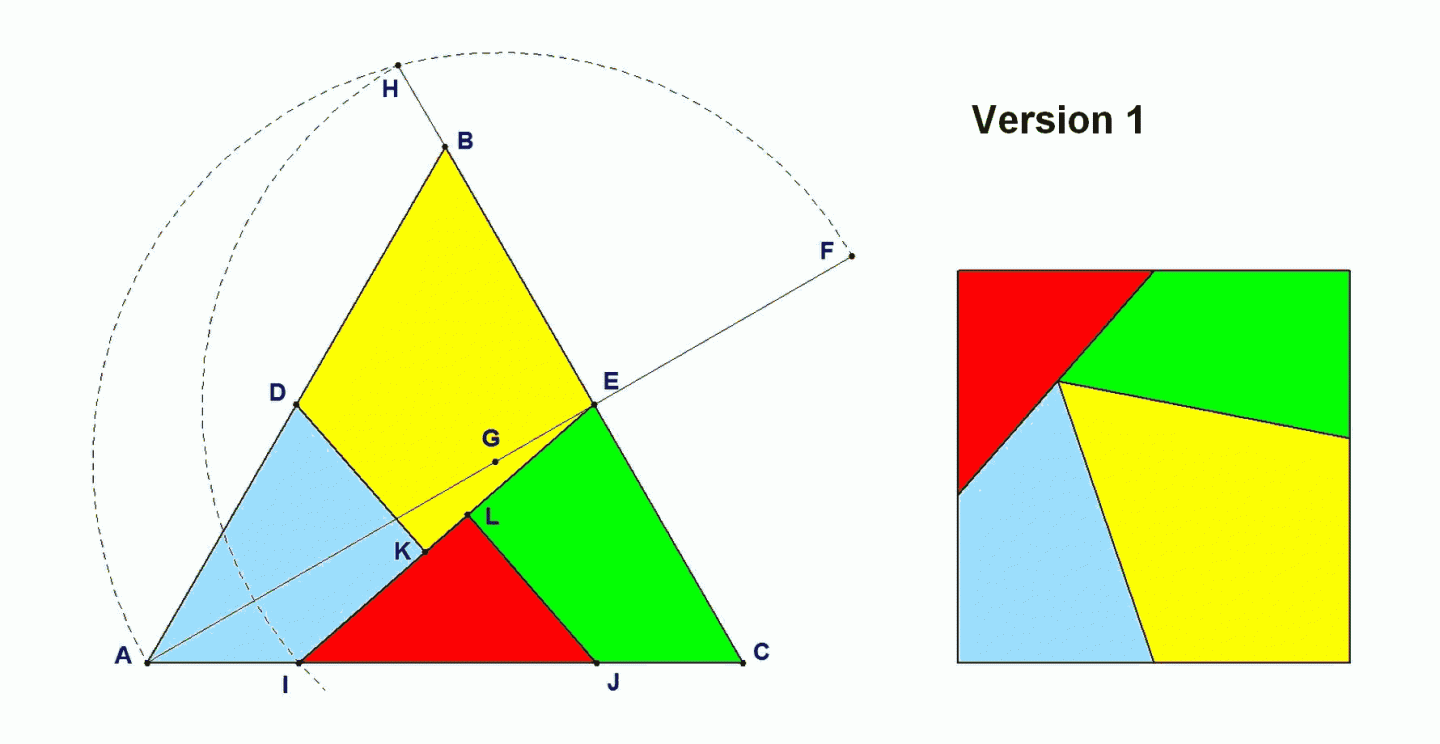
- Het midden van AB is D en van BC is het E.
- Verleng AE to F zodat EF=EB.
- G is het midden van AF.
- Met G als middelpunt beschrijven we de boog AHF, waarbij H gelegen is op het verlengde van EB
- Met E als middelpunt tekenen we de boog HI.
- Construeer J op AC zodat IJ=BE
- Teken IE
- Teken uit D en J de loodlijnen op IE met voetpunten K and L.