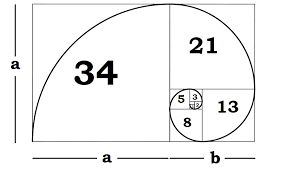
Fibonacci en de gulden snede | Wiskunde is leuk

De rij van Fibonacci: 1,1,2,3,5,8,13,21,… wordt gevormd door met twee enen te beginnen en dan is elke term de som van de vorige twee termen, dus:

$a_1=a_2=1 \text{ en } a_{n+2}=a_{n+1}+a_n$

Vorm nu de rij $s_n$ door twee opeenvolgende termen van de rij van Fibonacci te delen door elkaar:

$s_n=\frac{a_{n+1}}{a_n}$

Een paar termen van die rij zijn : $1,2,\frac{3}{2},\frac{5}{3},\frac{8}{5},...$ . Wat zou de limiet van deze rij nu zijn?

We vermoeden dat deze limiet bestaat. Noteer de limiet met L.
Nu geldt $s_n=\frac{a_{n+1}}{a_n}=\frac{a_n+a_{n-1}}{a_n}=1+\frac{1}{s_{n-1}}$ . Dus voldoet de limiet L aan de betrekking $L=1+\frac{1}{L}$ . Dit geeft de vergelijking

$L^2-L-1=0$

De positieve oplossing van deze vergelijking is $\frac{1+\sqrt{5}}{2}=\varphi=1,6180 3398 8749 8948 482...$ , de gulden snede!