Je beschikt over 7 verschillende flessen wijn en je hebt 7 proevers.  Het is niet praktisch alle 7 proevers alle 7 flessen te laten beoordelen, dus besluiten we volgende test te doen:

• Iedereen proeft van  eenzelfde aantal flessen.
• Elk paar van flessen wordt door exact 1 gemeenschappelijke persoon geproefd.
• Elk paar van proevers proeft exact 1 gemeenschappelijke wijn.

Kan die test worden uitgevoerd? En wat als je de 7 vervangt door een ander aantal? Dit type van problemen is van groot belang voor statistici en behoort tot de tak van de combinatorische ontwerp theorie. Voor 7 is het probleem oplosbaar. Geef de 7 proevers een nummer van 1 tot 7 en de flessen een label A tot G. De test kan dan worden uitgevoerd door iedereen 3 flessen te laten proeven:
1:{A,B,C}   2:{A,D,F}   3: {B,D,E}   4:{A,E,G}   5: {C,E,F}    6:{B,F,G}   7:{C,D,G}

Deze oplossing heeft ook een mooie grafische voorstelling in volgende figuur waar de proevers voorgesteld worden door lijnen en de flessen door punten. Je moet dus 7 lijnen tekenen tussen 7 punten zodat elk paar punten juist 1 lijn gemeen heeft en zodat elk paar lijnen juist 1 punt gemeen heeft.

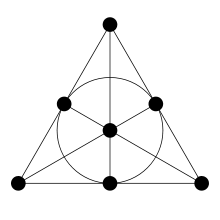
Je kan in ons voorbeeld 7 veranderen door een getal n van de vorm : met q een priemmacht. De overeenkomstige voorstelling geeft dan een projectief vlak van orde q+1. Dit vlak heeft  punten en  lijnen . Elke lijn bevat juist q+1 punten en door elk punt gaan exact q+1 lijnen. In bovenstaand voorbeeld is .