Beschouw in het vlak de punten P(x,y) met natuurlijke getallen als coördinaten .Je kan je verplaatsen in het vlak volgens de vectoren (1,0) , (0,1) en (1,1). Het aantal manieren waarop men vanuit de oorsprong het punt P(m,n) kan bereiken noemt men het Delannoy getal d(m,n), vernoemd naar de Franse legerofficier en amateur wiskundige Henri-Auguste Delannoy (28 sept 1833 – 5 febr 1915). Bij definitie stellen we d(0,0)=1.
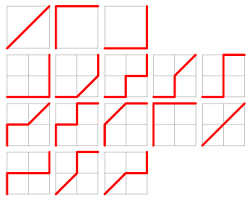
Onderstaande tekening laat zien dat er bijvoorbeeld 13 mogelijke manieren zijn om het punt P(2,2) te bereiken:
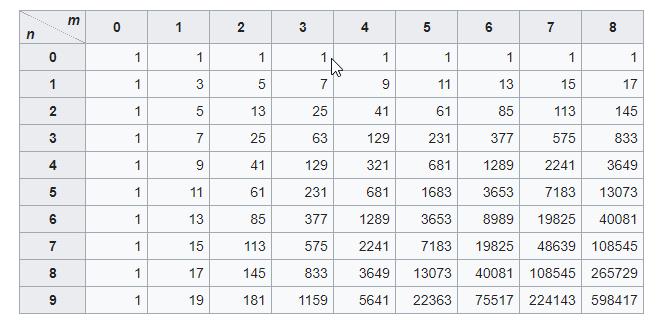
Een tabel met enkele waarden van de Delannoy getallen :
We geven enkele eigenschappen:
- d(m,0) = d(0,n) = 1
- Er is een recursief verband tussen deze getallen: d(m,n) = d(m – 1,n) + d(m,n – 1) + d(m – 1,n – 1): elk getal in bovenstaande tabel is de som van zijn linkerbuur, zijn bovenbuur en het getal linksboven. Dit wordt beter geïllustreerd als we de tabel geven in de vorm van de driehoek van Pascal. ( teken de diagonalen van bovenstaande tabel). Nu is elk getal de som van de driehoek erboven.

- We stellen de verplaatsingen over (1,0), (0,1) en (1,1) respectievelijk voor door O,N en D. Wanneer we k keer D gebruiken om P(m,n) te bereiken, moeten we m – k keer O en n – k keer N gebruiken. Om te berekenen op hoeveel manieren dit kan, maken we gebruik van de formule van de herhalingspermutaties : we moeten
k + (m – k) + (n – k ) = m + n – k symbolen rangschikken, waarvan er k van het soort D zijn , m – k van het soort O en n – k van het soort N. We vinden dus voor elke waarde van k kleiner of gelijk aan het minimum van m en n als aantal mogelijkheden:![Rendered by QuickLaTeX.com \[\dfrac{(m+n-k)!}{k! (m-k)! (n-k)!}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-43bad32dd4a8a540bb903884f5ef383a_l3.png?media=1678572382)
In het totaal heb je dan :
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{ min(m,n)}\dfrac{(m+n-k)!}{k! (m-k)! (n-k)!}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-3ccd7347c9ba955bb4a8b994358c565f_l3.png?media=1678572382)
- Op de tweede rij en tweede kolom vinden we alle oneven getallen :
d(m,1) = 2m+1. Dit is gemakkelijk te bewijzen met bovenstaande formule