Laten we het eens hebben over deze ‘rare’ figuur.

Neem  een rechthoekige strook papier:

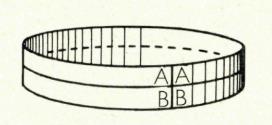
Door de uiteinden aan een te plakken ( uiteinde A aan uiteinde A) krijgen we een cilinder:

Deze cilinder heeft twee randen: een bovenrand en een onderrand en verder een binnen oppervlak en een buiten oppervlak. Deze worden als aparte objecten bekeken ( zie stippellijn en volle lijn). Van de binnenzijde kom je naar de buitenzijde via een rand.

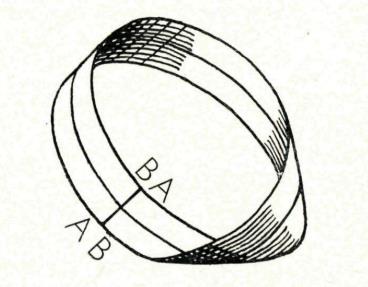
Je kan de strook echter ook op een andere manier aan elkaar lijmen ( uiteinde A aan uiteinde B):

Er is nu geen boven of onderkant. Deze figuur heeft maar 1 kant en 1 zijde. We noemen deze figuur de Möbiusband naar de Duitse wiskundige August Möbius(1790-1868).

Het bestuderen van dergelijke figuren maakt deel uit van de topologie, een tak van de wiskunde die zich bezighoudt met eigenschappen  die bewaard blijven bij continue vervorming (de objecten mogen niet worden gescheurd of geplakt). Anders dan de meetkunde, houdt de topologie zich niet bezig met metrische eigenschappen zoals de afstand tussen punten, maar met eigenschappen die beschrijven hoe een ruimte is samengesteld, zoals samenhang en oriëntatie.