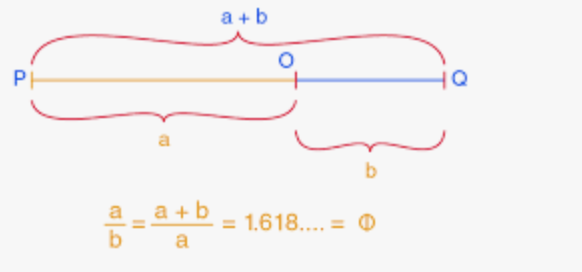
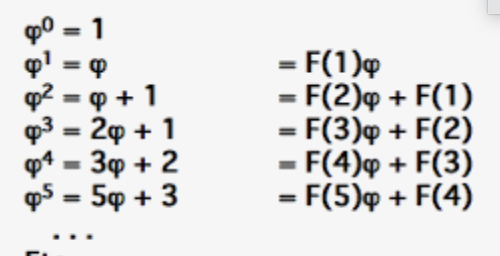De gulden snede en de rij van Fibonacci

Geplaatst op door

We kennen allemaal de gulden snede. Bij de gulden snede verhoudt het grootste van de twee delen van een lijnstuk zich tot het kleinste, zoals het gehele lijnstuk zich verhoudt tot het grootste. 

Maar er is ook een verband tussen \varphi en de rij van Fibonacci. Noteren we het n-de getal in deze rij door F(n).

  • Als we in bovenstaande uitdrukking \frac{a}{b} vervangen door \varphi, dan vinden we dat \varphi^2=\varphi+1.
  • Maar dat is \varphi^3=\varphi^2+\varphi=2\varphi+1.
  • Dus \varphi^4=2\varphi^2+\varphi=3\varphi+2.
  • Algemeen kan men dan stellen dat :

        \[\varphi^n=F(n)\varphi+F(n-1)\]