Categorie archieven: Weetjes

22/7

Geplaatst op door

Vroeger vertelde men ons dat we voor \pi de breuk \frac{22}{7} mochten nemen. Natuurlijk drong het niet bij iedereen door dat dit een benadering was. Een bewijsje:

Neem de functie

    \[f(x)=\frac{x^4(1-x)^4}{1+x^2}\]

  • f is strikt positief en continu tussen 0 en 1.
  • Dus is \int_0^1f(x) dx>0.
  • De Euclidische deling geeft \frac{x^4(1-x)^4}{1+x^2}=x^6-4x^5+5x^4-4x^2+4-\frac{4}{1+x^2}.
  • Een primitieve functie van f is dan \frac{1}{7}x^7-\frac{4}{6}x^6-x^5-\frac{4}{3}x^3+4x-4\text{Bgtan }(x).
  • Bijgevolg is \int_0^1f(x) dx= \frac{22}{7}-\pi. 
  • Uit het tweede puntje volgt dan:
  • Narekenen op rekentoestel geeft \frac{22}{7}=3,142857142857,... en \pi=3,14159265....

9801

Geplaatst op door

Mooie decimale schrijfwijze! Kan je dit verklaren?

Nu is \frac{1}{99}=0,01010101...=\sum_{n=1}^{\infty}\frac{1}{100}. Verder is \frac{1}{9801}=\Big(\frac{1}{99}\Big)^2.

Je kan gemakkelijk narekenen dat

    \[\Big(\sum_{n=1}^{\infty}x^n\Big)^2=x.\sum_{n=1}^{\infty}nx^n\]

Vervangen we nu hierin x door \frac{1}{99}, dan krijgen we de gewenste decimale schrijfwijze. Maar waarom ontbreekt hierin de 98?

In de uitwerking staan de som \frac{98}{100^{98}}+\frac{99}{100^{99}}\frac{100}{100^{100}}=\frac{1}{100^{100}}(980000+9900+100)=\frac{99}{100^{98}}. 

Wat gebeurt er met \frac{1}{998001} en \frac{1}{99980001}?

Hoe lang zal de wereld bestaan?

Geplaatst op door

In de grote tempel van Benares, onder de koepel die het centrum van de wereld aangeeft, staat een grote bronzen plaat, waarin drie diaman­ten naalden zijn bevestigd, elk ter lengte van een onderarm en zo dik als het lichaam van een bij.
Op één van deze naalden plaatste God bij de Schepping vierenzestig schijven van zuiver goud. De grootste rustte op de bronzen plaat, de volgende werden naar boven toe steeds kleiner. Dit is de toren van Brahma.

Dag en nacht, zonder onderbreking, verplaatsen de priesters de schijven van de ene naald naar de andere, overeenkomstig de vaste en onveranderlijke wetten van Brahma, volgens welke de dienstdoende priesters niet meer dan één schijf tegelijk mogen bewegen en geen schijf geplaatst mag worden op een naald die al een kleinere schijf bevat. Als de vierenzestig schijven van de naald waarop God ze bij de Schepping plaatste, overgebracht zullen zijn naar één van de andere, dan zullen de torens en de tempel en de priesters tegelijk tot stof vervallen en met een donderslag zal de wereld vergaan.”

Hoe lang moeten de priesters werken, als ze zonder ooit een fout te maken elke seconde één schijf overbrengen?

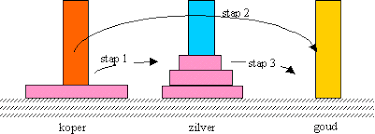Je kan dit proces heel gemakkelijk recursief beschrijven:  Met n schijven: los het probleem op door de bovenste n-1 schijven naar pin B te brengen, met pin C als hulppin. Vervolgens wordt -n-de schijf naar pin C gebracht. Tot slot worden de eerste n-1   schijven van pin B naar pin C gebracht, met pin A als hulppin. Als we met u_n het aantal zetten noteren om n schijven van één pin naar een andere te zetten , dan geldt:

    \[u_n=2u_{n-1}+1\]

We kunnen dit omzetten naar het expliciet voorschrift u_n=2^n-1. De wereld zal dus 2^{64}-1 jaren bestaan, dat is zo ongeveer duizend miljard jaar. Als het verhaal klopt natuurlijk….

Als spel werd dit onder de naam Torens van Hanoi op de markt gebracht in 1863 door Edouard Lucas, onder de schuilnaam prof Claus.

Stelling van Zeckendorf

Geplaatst op door

De stelling van Zeckendorf  is vernoemd naar de Belgische dokter, legerofficier en wiskundige Edouard Zeckendorf.

De stelling zegt dat elk positief geheel getal op een unieke manier kan geschreven worden als de som van één of meer verschillende  getallen uit de rij van Fibonacci die elkaar niet opvolgen. Een dergelijke som wordt de Zeckendorfrepresentatie van een getal genoemd. De Zeckendorfrepresentatie van het getal 100 is 89+8+3.

Start met het grootste getal a_1 uit de rij van Fibonacci dat kleiner is of gelijk aan het getal n. Zoek daarna het grootste getal a_2 uit de rij van Fibonacci dat kleiner is of gelijk aan het verschil  n-a_1. Blijf dit proces herhalen totdat het verschil uiteindelijk zelf een getal is uit de rij van Fibonacci. Nu zijn a_1 en a_2 geen opeenvolgende termen van de rij van Fibonacci, want waren ze dat wel dan zou a_1+a_2 een term van de rij van Fibonacci zijn en groter zijn dan n. Dit is onmogelijk want a_1+a_2<n.

We geven ook een Python programma mee om de Zeckendorf representatie te berekenen. In het voorbeeld berekenen we deze van 2021: