1 mijl( = 1 mi ) is 1,609344 km, wat dicht bij het gulden getal 
ligt. De waarde van 
wordt benaderd door de verhouding van twee opeenvolgende getallen in de rij van Fibonacci. Daarom kan je voor de omzetting van mijlen naar kilometer en omgekeerd gebruik maken van opeenvolgende Fibonacci getallen, met vrij grote nauwkeurigheid.
Er zijn met computationeel denken altijd meerdere mogelijke werkwijzen. De oplossing binnen wiskunde zal hetzelfde zijn voor de hele klas, maar elke leerling kan een eigen strategie kiezen of bedenken om tot die oplossing te geraken. Vanaf dat een kind praat, stelt het zelf alles in vraag “Waarom?”. Hoe jonger het kind, hoe kleiner we de deelstappen maken.”
Eerst wordt er een overzicht gegeven van het eindproduct ‘het grote probleem’ om vervolgens stap voor stap het probleem op te lossen. Er wordt stap voor stap, blok per blok gebouwd om tot het geheel te komen. Eigenlijk is dat computationeel denken. Oudere leerlingen zijn zelf in staat om te beslissen welke vragen ze zichzelf moeten stellen om tot het eindproduct te komen.
Wiskunde is het meest logische vak om computationeel denken aan te leren. Als heuristiek wordt een probleem opgelost door het stellen van deelvragen, denk aan het algoritme: gegeven, gevraagd, oplossing. Probleemoplossend denken is eigenlijk hetzelfde basisprincipe als computationeel denken. Het inzichtelijk leren of het leren door zichzelf vragen te stellen, stelt de leerling in staat inzicht te krijgen in het grote geheel.
De Amerikaanse onderzoekster Jeannette Wing introduceerde in 2006 het begrip computationeel denken als volgt:
“Computational thinking is reformulating a seemingly difficult problem into one we know how to solve, perhaps by reduction, embedding, transformation or simulation.”
Computationeel denken is daarom, volgens haar, een basisvaardigheid, die iedereen zou moeten beheersen, naast lezen, rekenen en schrijven.
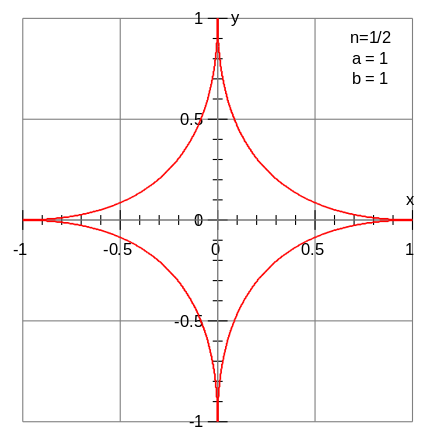
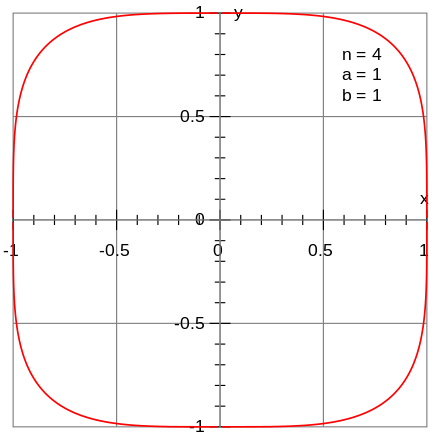
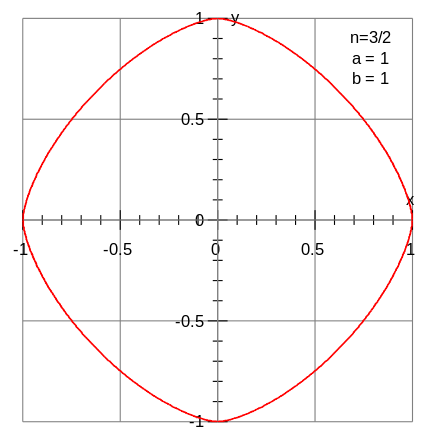
De krommen van Lamé zijn ellipsvormige krommen die voor het eerst gedefinieerd werden door de Franse wiskundige Gabriel Lamé in 1818.
Ze worden gedefinieerd door de vergelijking:
![\[|\frac{x}{a}|^n+|\frac{y}{a}|^n=1\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-be734640dd867ef6cda24eb8eb216299_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
Een paar voorbeelden:
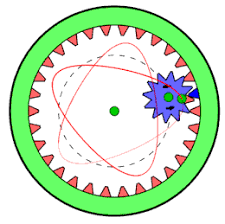
Een spirograaf is een instrument dat gebruikt wordt om geometrische figuren te tekenen. De spirograaf werd bedacht door Denys Fisher ( 1918-2002), een Engelse ingenieur. Het instrument bestaat uit een aantal tandwielen en een aantal andere voorwerpen, zoals ringen, driehoeken, rechte strips, ook voorzien van vertanding langs de rand (en in geval van de ringen ook langs de binnenkant). De onderdelen kunnen met spelden op de ondergrond worden vastgeprikt en andere onderdelen kunnen door middel van de vertanding langs een vastgeprikt voorwerp rollen. In de onderdelen bevinden zich diverse gaatjes waardoor een potlood of pen met dunne punt kan worden gestoken. Door de stralen van de schijven en de positie van het gaatje te variëren kunnen tal van patronen worden vervaardigd.
Door de stralen van de schijven en de positie van het gaatje te variëren kunnen tal van patronen worden vervaardigd.
Neem een willekeurig getal, zeg 56 en vermenigvuldig de cijfers. dan bekom je 5*6=30. Bij dit getal neem je opnieuw het product van de cijfers: 3*0=0. Als je nu verder zou gaan met het product van de cijfers te nemen, dan verandert er niets meer. Na 2 stappen bekom je dus een getal van 1 cijfer. We noemen 2 de volhardingswaarde van het gegeven getal 56.
Algemeen: Neem dus een willekeurig getal, vermenigvuldig alle cijfers met elkaar, zodat je een nieuw getal krijgt. Als dat getal meerdere cijfers bevat, herhaal je het proces van cijfers vermenigvuldigen, totdat je maar 1 cijfer over houdt. Het aantal stappen dat je daarvoor nodig hebt noem je de volhardingswaarde van het gegeven getal.
Een programma in Python:
Is er een maximaal aantal stappen voor een willekeurig getal? Dit ‘eenvoudig’ probleem werd bedacht door Neil Sloane, een Amerikaanse wiskundige.
We kennen hem het best van zijn website (oeis.org) met zijn verzameling getallenreeksen. In 1973 schreef hij in Journal of Recreational Mathematics een artikel over het probleem van de volhardingswaarde. Hij beweerde dat we maximaal 11 stappen kunnen maken eer we een enkel cijfer over houden, hoe groot het begin getal ook is. Dit vermoeden werd tot op heden nog niet bewezen.
Het kleinste getal met volhardingswaarde 1 is uiteraard 10. Verder is 25 het kleinste getal met volhardingswaarde 2, 39 het kleinste getal met volhardingswaarde 3, 77 het kleinste getal met volhardings-waarde 4 en 679 het kleinste getal met volhardingswaarde 5.
De kleinste getallen met volhardingswaarden 6,7,8,9,10 en 11 zijn respectievelijk 6788,68889,2677889,26888999,3778888999 en 277777788888899.