Categorie archieven: Weetjes

Afstanden

Geplaatst op door

We kennen allemaal het visueel evidente begrip afstand  als ” de lengte van het deel van de rechte lijn tussen twee punten”, dat  ontleend is aan de klassieke meetkunde. Daarbij bleef de term “rechte lijn” zelf ongedefinieerd of hoogstens werd er gezegd dat het de kortste weg was tussen twee punten, waarmee men in een cirkelredenering terecht kwam.

Bovendien is de afstand langs de rechte lijn niet altijd geschikt voor het oplossen van veel praktische en theoretische problemen.

  1. Een transportfirma is bij het opstellen van een vervoersplan niets gebaat met de kennis van de afstanden in vogelvlucht tussen vertrek en aankomst, daar de vrachtwagens verplicht zijn het bestaande verkeersnet te volgen.
  2. Een schip of vliegtuig is tijdens zijn reis verplicht de kromming van de aarde te volgen, daar het nu eenmaal niet mogelijk is in een rechte lijn door de aardkorst te boren.
  3. Hoe zou je bijvoorbeeld de afstand tussen twee functies ( nodig bij het bestuderen van de convergentie van een rij van functies)  kunnen definiëren?

In de wiskunde is een begrip afstand of metriek gedefinieerd als generalisatie van het gewone afstandsbegrip. Deze generalisatie is zo gekozen dat een aantal kenmerkende eigenschappen van het gewone afstandsbegrip behouden blijven.

Een afstand of metriek in een verzameling V is een afbeelding d  die met twee elementen uit  V een getal laat associëren die de volgende eigenschappen bezit:

  1. De afstand is positief: d(x,y) \geq 0.
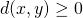  2. x ligt even ver van y als y van x ( symmetrie ): d(x,y)=d(y,x).
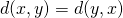  3. Een omweg maken is steeds langer dan de rechtstreekse weg te nemen
    ( driehoeksongelijkheid ):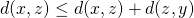 d(x,z) \leq d(x,z)+d(z,y)
  4. Iedere x ligt op een afstand 0 van zichzelf: d(x,x)=0
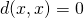
  5. Het omgekeerde van vorige eigenschap: d(x,y)=0 \leftrightarrow x=y

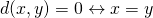
Een paar voorbeelden in het vlak:

  • De Euclidische afstand of metriek, gegeven door 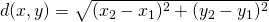d(x,y)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} komt overeen met ons klassiek begrip afstand.
  • De Manhattan metriek,voor het eerst onderzocht aan het eind van de 19e eeuw door Hermann Minkowski, en wordt gegeven door 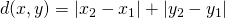d(x,y)=|x_2-x_1|+|y_2-y_1|  De naam verwijst naar de roostervormige opzet van de meeste lanen en straten op het eiland Manhattan, zoals vastgelegd in een plan uit 1811. Dit rooster zorgt ervoor dat de kortste route die een voetganger of auto kan nemen om de afstand tussen twee punten in de stad te overbruggen een lengte heeft die gelijk is aan de afstand tussen twee punten in de Manhattan-metriek. In onderstaande tekening zijn de lijnen in rood, geel en blauw  drie voorbeelden van de Manhattan-afstand tussen de twee zwarte, ronde punten. Zij zijn alle drie 12 eenheden lang. De groene lijn stelt de volgens de Euclidische afstand kortste route voor tussen de twee punten.
    Een ander voorbeeld kan je ook vinden in de codetheorie , waar men de Hamming-afstand definieert door het aantal posities te tellen waar de twee binaire codes van elkaar verschillen

 

Het tovervierkant van Lo Shu

Geplaatst op door

Een tovervierkant is een vierkantig rooster van getallen zodat de som van de elementen op elke rij, kolom en diagonaal hetzelfde is. Het oudste tovervierkant wordt toegeschreven aan Lo Shu en dateert van omstreeks 2200 voor onze tijdrekening. Hij was gekerfd in het schild van een schildpad in de Lo-rovier.

Of in matrixvorm :

Als we deze matrix L noemen , kunnen we ook L² en L³ uitrekenen:

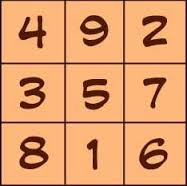
    \[L^2 =\begin{pmatrix} 59&83&83\\83&59&83\\83&83&59\end{pmatrix}\]

    \[L^3=\begin{pmatrix}1149&1029&1197\\1173&1125&1077\\1053&1221&1101\end{pmatrix}\]

De matrix L^2 is symmetrisch en is een pseudo-tovervierkant ( de som van de elementen op elke rij en in elke kolom is dezelfde; de sommen van de diagonalen echter niet ).

De matrix L^3 is dan weer wel een tovervierkant, maar de symmetrie is verdwenen.

Wiskundig denken

Geplaatst op door
Wiskundig denken is de kern en de kracht van wiskunde

 

Wat is nu dat wiskundig  denken? De Nederlandse wiskundige P.Drijvers geeft volgende omschrijving:

Bedenken hoe je  wiskundig gereedschap kan gebruiken om een probleem op te lossen.

  • Hoe? : hier bedoelen we de keuze van de gereedschappen die je gaat gebruiken, in welke volgorde je dat doet en onder welke voorwaarden ze zinvol kunnen gebruikt worden.
  • Wiskundig gereedschap? : dit moet breed worden opgevat. het kan heel specifiek en concreet zijn, zoals de formule van Pythagoras, maar ook theoretisch ( logisch redeneren, bewijzen), of algemeen van karakter ( het ontwikkelen van strategieën).
  • Gebruiken? : niet allen het toepassen van een bestaande, kant-en-klare methode, maar ook het ontwikkelen ervan, of het op maat maken van een bestaande methode voor een specifiek doel.
  • Probleem? : dit is niet zomaar een opgave, maar wel een vraag waar je geen kant-en-klare oplosmethode ter beschikking hebt

 

Je kan drie kernaspecten beschouwen: probleemoplossen, modelleren en abstraheren.

Wat voor iemand een probleem is, dus wat niet standaard is voor hem of haar, hangt af van voorkennis en ervaring. Wiskundig denken is dus relatief: wat voor de ene uitdagend en nieuw is, zal voor de andere routinematige reproductie zijn.

Erlanger Programm van Felix Klein

Geplaatst op door

Felix Christian Klein (Düsseldorf, 25 april 1849 – Göttingen, 22 juni 1925) was een Duits wiskundige. Klein was hoogleraar aan de universiteiten van Erlangen, München, Leipzig en uiteindelijk Göttingen waar hij wiskunde doceerde. Zijn hoofdonderwerpen waren niet-euclidische meetkunde, groepentheorie en functietheorie. Naar hem is onder andere de fles van Klein genoemd. In 1912 kreeg hij de Copley Medal.

In 1872 hield hij zijn inaugurale rede aan de universiteit van Erlangen, beroemd geworden onder de naam Erlanger programm. Klein vond het noodzakelijk meetkunde te onderwijzen vanuit het groeptheoretisch standpunt. Dit betekent niet dat meetkunde moet vervangen worden door groepenleer, maar wel dat de eenvoudige begrippen en eigenschappen uit die theorie zouden gebruikt worden als verhelderende en ordenende elementen bij de opbouw van de meetkunde. Vanaf begin 20 ste eeuw werd algemeen aanvaard een meetkunde te definiëren als een invariantentheorie van een bepaalde transformatiegroep. In feite zegt Klein dat om aan meetkunde te doen twee dingen nodig zijn: een verzameling punten en een transformatiegroep. Meetkunde is de studie van de invarianten onder deze transformaties. Wanneer we iets aan de verzameling, of aan de groep veranderen hebben we een andere meetkunde. Alles wat niet invariant is is in feite onbelangrijk.

 

De paradox van Simpson.

Geplaatst op door

De Franse wiskundige B.Pascal legde omstreeks 1650 samen met Pierre de Fermat de grondslagen voor de kansrekening. Het berekenen van winstkansen is echter niet zo eenvoudig en je komt bij de toepassingen verschillende schijnbare tegenstellingen tegen.

Deze paradox is genoemd naar de statisticus E.H.Simpson en werd in 1951 voor het eerst gepubliceerd. Laten we die paradox  bespreken aan de hand van een voorbeeld.

In bovenstaande tabel staan de slaagcijfers van jongens en meisjes voor 3 studierichtingen: medische, humane en exacte wetenschappen. Uit deze tabel blijkt dat in de 3 verschillende richtingen de slaagpercentages van de meisjes net iets hoger liggen dan bij de jongens. Paradoxaal genoeg blijken de jongens in het totaal toch beter te presteren dan de meisjes: 51% tegen 46%.

De verklaring is dat meisjes zich meestal inschreven voor studierichtingen waar de slaagkansen kleiner waren. Dit is Simpsons paradox: als je gegevens van twee groepen op een onhandige manier combineert, dan lijken de resultaten van de groepen om te draaien.