De vraag die we willen behandelen in deze tekst luidt:
Construeer het rekenkundig gemiddelde ( RG) en het harmonisch gemiddelde (HG) van de twee evenwijdige zijden van een trapezium.
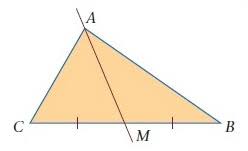
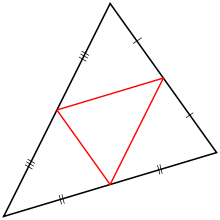
- Her RG is vrij eenvoudig: construeer het lijnstuk door de middens van de opstaande zijden. Volgens de stelling van Thales is
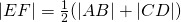
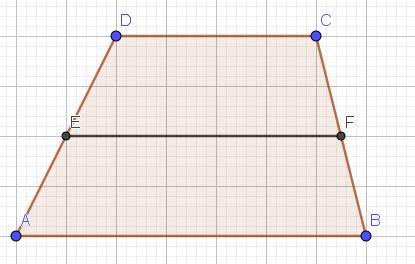
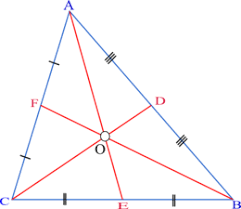
- Voor het harmonisch gemiddelde construeren we het lijnstuk, evenwijdig aan de evenwijdige zijden, door het snijpunt van de twee diagonalen van het trapezium.
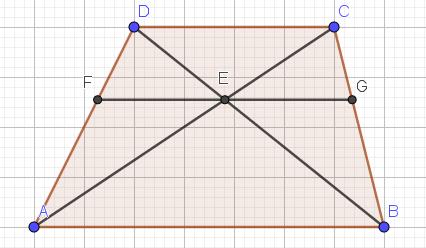 Uit de gelijkvormigheid van de driehoeken FDE en ADB, CEG en CAB, DEC en EAB volgt dat
Uit de gelijkvormigheid van de driehoeken FDE en ADB, CEG en CAB, DEC en EAB volgt dat  . Construeer nu , door C, een evenwijdige aan AD. Noteer
. Construeer nu , door C, een evenwijdige aan AD. Noteer  en
en 
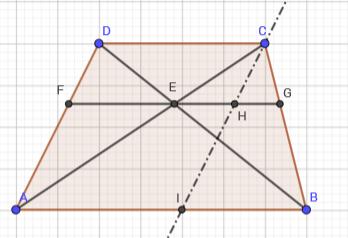 Nu is
Nu is 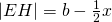 en
en  . De 3 concurrente rechten AC,IC en BC worden gesneden door 2 evenwijdige rechten, dus geldt volgens Thales dat
. De 3 concurrente rechten AC,IC en BC worden gesneden door 2 evenwijdige rechten, dus geldt volgens Thales dat 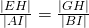 of
of 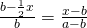 . Hieruit volgt dat
. Hieruit volgt dat  en dit betekent dat
en dit betekent dat  het harmonisch gemiddelde is van de twee evenwijdige zijden van het trapezium.
het harmonisch gemiddelde is van de twee evenwijdige zijden van het trapezium.