Categorie archieven: Weetjes

Geschiedenis van 0

Geplaatst op door

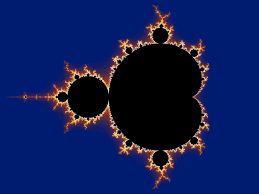
Wat zou de wereld zijn zonder het getal 0? Wat was dan de uitkomst van de bewerking 5 – 5? En hoe hadden we dan onderscheid gemaakt tussen één, tien, honderd en duizend? Zouden er dan computers en internet zijn? Alle digitale gegevens worden immers opgebouwd uit eentjes en nulletjes.

Een soort nul  werd al toegepast door de Babyloniërs rond 450 v.Chr. Zij duidden een lege plaats in een rij met cijfers aan met twee wiggen. Het getal nul kenden ze echter niet.  Ook de Maya’s hadden de nul ontdekt, vanuit de vrees dat er ooit een einde zou komen aan de tijd. De Egyptenaren, Grieken en Romeinen gingen aan het cijfer voorbij, met als gevolg dat de christelijke tijdskalender niet zoiets heeft als het jaar nul. Wij beginnen immers met het jaar 1 (volgend op 1 voor Christus).

De oudst bekende tekst die een decimaal positiestelsel gebruikte, inclusief de nul, is een tekst uit India genaamd Lokavibhaaga, uit 458 n.Chr. Het eerst bekende gebruik van een speciale teken voor decimale cijfers met in de grond het uiterlijk van het moderne cijfer, een kleine cirkel, is te vinden op een stenen inscriptie gevonden bij de Chaturbhujatempel in Gwalior in India, daterend uit het jaar 876. 

Door het gebruik van de Arabisch-Indische cijfers werd het plotseling mogelijk om hele grote getallen op te schrijven. Met de Romeinse cijfers kon dat niet: om van één naar duizend te tellen waren al zeven tekens nodig en bij hogere getallen nog meer. In het Arabisch-Indische maximaal tien. Toch was Europa het getal nooit gaan gebruiken als het aan de Romeinen had gelegen. De Romeinse keizers wilden namelijk vasthouden aan hun eigen cijfers. Zij boden daarom fel weerstand tegen het cijfersysteem dat overwaaide uit het Midden-Oosten. Dat de 0 toch in Europa belandde, is te danken aan de Moren. Zij veroverden in de achtste eeuw na christus grote delen van het huidige Spanje en Portugal en brachten de Arabisch-Indische cijfers (0 tot 9) met zich mee. Verschillende wetenschappers, onder wie de Italiaan Fibonacci in de twaalfde eeuw, droegen vervolgens bij aan de populariteit van het cijfersysteem. 

 

Fractaal ontsnappingsspel

Geplaatst op door
Beantwoorden

Peter is een geheim agent die gevangen gehouden wordt door terroristen Hij heeft een ontsnappingsplan: volg de kwadratische vergelijking z_{n+1}=z_n^2+c, waarbij de vloer van zijn kamer als het complexe vlak wordt bekeken en waar hij in de oorsprong staat.  Peter kent echter de constante c niet. Voor welke waarden van c heeft hij een kans op ontsnapping?

                                                 

Proberen we eerst c = 0. Maar dan wordt, voor elke n, z_n=0 en blijft hij steeds op dezelfde plaats. Als we andere waarden van c proberen, zijn er 3 mogelijkheden:

  1. De rij z_n convergeert naar een vast punt.
  2. De rij z_n wordt herhaald in een eindige cyclus van punten en wordt een periodieke rij.
  3. De rij z_n divergeert weg van de oorsprong en Peter heeft kans op ontsnapping.

Dit verhaal is eigenlijk het verhaal van de Mandelbrot verzameling, namelijk de verzameling van alle complexe getallen c waarvoor de baan van z_{n+1 }=z_n^2+c begrensd is ( dus niet divergeert) met startpunt (0,0).

Perfecte getallen

Geplaatst op door

Wiskundigen zijn vaak geboeid door speciale eigenschappen van getallen. Zo kennen we bijvoorbeeld perfecte getallen, dit zijn positieve getallen n waarvan de som van de delers ( genoteerd door \sigma(n), tweemaal het getal is.

Voorbeelden zijn :
\sigma(6) = 1 + 2 + 3 + 6=12
\sigma(28)=1+2+4+7+14+28=56
Zo zijn ook 496 en 8128 perfect. Deze 4 voorbeelden zijn allen even. De enige gekende perfecte getallen zijn inderdaad even. Hieromtrent kennen we volgend resultaat:
Als 2^n-1 een priemgetal is , dan is a=2^{n-1}(2^n-1) perfect en elk even perfect getal is van die vorm.

Het is een open probleem of er ook oneven perfecte getallen bestaan.

Reeds in de tijd van  Pythagoras werden  perfecte getallen onderzocht. Perfecte getallen hadden in die tijd een religieuze betekenis. In de beginjaren van het christendom was er een theorie dat de getallen 6 en 28 door God gekozen waren als perfecte getallen: 6 is het aantal dagen waarin God de aarde had geschapen en 28 is het aantal dagen waarin de maan om de aarde draait. De heilige Augustinus (354-430) schreef: Zes is geen perfect getal omdat God de aarde in zes dagen geschapen heeft, maar God heeft de aarde in zes dagen geschapen omdat zes een perfect getal is.

Nicomachus van Gerasa vermeldde rond het jaar 100 in zijn boek Introductio Arithmeticae een aantal resultaten ( niet noodzakelijk waar) zoals: Het n-de perfecte getal heeft n cijfers; Alle perfecte getallen zijn even; Perfecte getallen eindigen afwisselend op een 6 of een 8; Er zijn oneindig veel perfecte getallen. Deze stellingen zijn in Europa eeuwenlang voor waar aangenomen. De Europeanen waren gedurende de vroege Middeleeuwen onbekend met het wiskundig onderzoek in de Arabische landen, onder andere dat van Ibn al–Haytham en van Ismail ibn Ibrahim ibn Fallus. Deze laatste wiskundige stelde in het begin van de 13e eeuw een lijst op met tien perfecte getallen, waarvan de eerste zeven inderdaad juist zijn, maar deze lijst raakte pas eeuwen later in Europa bekend.

Een nieuwe algebra

Geplaatst op door

Een algebra is eigenlijk een verzameling uitgerust met één of meerdere bewerkingen. We kennen allemaal getallenverzamelingen met daarin een optelling en een vermenigvuldiging. Maar je kan ook een algebra definiëren in een verzameling zonder getallen. Neem bijvoorbeeld de verzameling punten in het vlak (a,b,c,…) en de bewerking a.b =c met c het midden van [a,b] en a.a=a.

  • Het is een binaire bewerking: met twee punten komt terug een punt overeen.
  • Deze bewerking is commutatief : a.b=b.a want het midden van [a,b] is hetzelfde als het midden van [b,a].
  • De bewerking is niet associatief: meestal is a.(b.c) niet gelijk aan (a.b).c. We kunnen de haakjes in uitdrukkingen van de vorm (a.b).c dus niet weglaten.
  • We kunnen ook vergelijking van de vorm a.x=b oplossen. We noteren de oplossing als \frac{b}{a}.
  • We moeten goed oppassen om rekenregels die we kennen uit de getallenleer, niet zomaar over te dragen naar deze nieuwe algebra. Zo is \frac{a}{b}.\frac{c}{d}=\frac{a.c}{b.d} maar is a.\frac{b}{c} niet gelijk aan \frac{a.b}{c}.

Rekenen in dergelijke wiskundige structuur is zeer boeiend en is onderdeel van de abstracte algebra waarin begrippen zoals groepen, ringen, velden, vectorruimten e.d. gebruikt worden om bepaalde ‘algebra’s’met zelfde eigenschappen samen te brengen.

 

Fermat priemgetallen en regelmatige veelhoeken

Geplaatst op door

De Franse wiskundige Pierre de Fermat( 1601-1665) dacht dat alle getallen van de vorm 2^{2^n} priemgetallen waren. En voor de eerste 5 waarden van n was dat ook zo:

\begin{array}{c|c} n& 2^{2^n} \\ \hline\\ 0 &3\\1&5\\2&17\\3&257\\4&65.537\end{array}

Later ontdekte Leonard Euler( 1707-1783) in 1732 dat het Fermat getal voor n = 5 ontbonden kon worden als  4.294.967.297 = 641 x 6.700.417. En hier zou het verhaal dan stoppen, ware er niet de geniale ontdekking van Carl Friedrich Gauss(1777-1855).

In 1794 vond Gauss dat een regelmatige veelhoek met p zijden (met p een priemgetal ) construeerbaar is met passer en liniaal als en slechts als p een Fermat priemgetal is, dus een priemgetal van de vorm 2^{2^n}. Als eerbetoon werd in Brauschweig, de thuisstad van Gauss,  een bronzen standbeeld opgericht waar hij staat op een regelmatige zeventien hoek.

Welke regelmatige veelhoeken zijn dan construeerbaar met passer en liniaal? Volgens Gauss’ resultaat zijn dat de gelijkzijdige driehoek, de regelmatige 5-hoek, de regelmatige 17-hoek, de regelmatige 257-hoek en de  regelmatige 65.537-hoek. We weten dat ook de regelmatige veelhoeken met 7,11,13,19,… zijden niet construeerbaar zijn omdat het wel priemen zijn, maar geen Fermat priemen. Verder zijn ook regelmatige veelhoeken met 4,8,16,32,.. en 6,12,24,48,… zijden construeerbaar omdat we met passer en liniaal een hoek in twee kunnen verdelen. En wat met de anderen? Is een regelmatige 15 hoek construeerbaar?  Het blijkt van wel, omdat \frac{1}{15}=\frac{2}{5}-\frac{1}{3} en dus kunnen we een cirkel in 15 gelijke delen verdelen.

Het was uiteindelijk Pierre Wantzel die in 1837 volgend algemeen reultaat bewees: Een regelmatige n-hoek is construeerbaar met passer en liniaal als en slechts als n het product is van een macht van 2 en een willekeurig aantal verschillende Fermat priemgetallen.