Charles Caleb Colton (1780–1832) was bekend vanwege zijn soms zeer scherpe quotes:
De studie van de wiskunde begint, net zoals de Nijl, klein en verfijnd maar eindigt groots en glorieus.
Categorie archieven: Weetjes
Stemparadox
In het zicht van de volgende verkiezingen, even wat uitleg over de stemparadox. De paradox duidt een situatie aan bij een stemming waarbij er geen manier bestaat om met de individuele voorkeuren een collectieve uitkomst te bepalen. Veronderstel de volgende voorkeuren bij 3 kiezers (I,II en III):
| 1ste keus | 2de keus | 3de keus | |
| I | Bart | Meyrem | Wouter |
| II | Wouter | Bart | Meyrem |
| III | Meyrem | Wouter | Bart |
Stel dat onze drie kiezers eerst moeten kiezen tussen Bart en Meyrem. Dan wint Bart door de stem van kiezers I en II. Maar als het vervolgens in de tweede ronde tussen Bart en Wouter gaat, dan wint Wouter door de stem van kiezers II en III. Nochtans haalt Meyrem het duidelijk van Wouter dankzij kiezers I en III… Ook voor de andere combinaties beland je in een lus. Nochtans heeft elk van de drie kiezers een duidelijke en consistente voorkeur. De stemparadox illustreert daarmee de relativiteit van sommige democratische beslissingen.
Deze paradox wordt ook wel de paradox van Condorcet genoemd en werd door de markies Nicolas de Condorcet(1743-1794) geformuleerd aan het einde van de 18de eeuw.
Diabolo
Een diabolo is een voorwerp waarmee men allerlei trucs kan uitvoeren. Het bestaat uit twee komvormige delen die met hun bodem aan elkaar zijn verbonden. Dit verbindingsstuk is het steunpunt voor de diabolo. Bij een diabolo horen twee stokjes bij die met een touw zijn verbonden. Hiermee kan de diabolo aan het tollen worden gebracht, zodat hij in balans blijft, en in de lucht kan worden gegooid en opgevangen. Het jongleren met een diabolo is afkomstig uit China.
Hoe kan je nu dergelijke figuur wiskundig genereren? Neem de impliciete vergelijking in de onbekenden x,y en z:
![\[x^2=(y^2+z^2)^2\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-4584b15e1ee5f1737fe25946c38a247a_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
Het is duidelijk dat dit oppervlak de unie is van twee omwentelingsparaboloïden: 
die elkaar raken in de oorsprong. Het raakvlak is het verticale vlak 
.
Bovenstaande tekening is gemaakt met het programma Surfer.
Hexomino’s
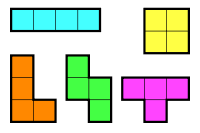
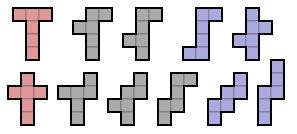
In 1953 introduceerde Solomon W. Golomb, toen student aan de Harvard Universiteit, de term polyomino voor figuren die gevormd worden door eenheidsvierkanten samen te voegen. Omdat een domino bestaat uit twee aaneengesloten vierkanten, stelde Golomb voor figuren met drie vierkanten tromino’s te noemen. Die met vier vierkanten tetromino’s. En verder pentomino’s, hexomino’s, heptomino’s enz.
Hoeveel hexomino’s zijn er nu en hoeveel ervan kan je tot een kubus bouwen? Figuren die door een draaiing of een spiegeling op elkaar kunnen afgebeeld worden, beschouwen we als identiek.
- De eenheidsvierkanten kunnen op verschillende manieren aaneengesmeed worden. Er is één monomino en één domino.
- Om het aantal tromino’s (ook wel triomino’s genoemd) te bepalen, zoeken we uit hoe we van een domino een tromino kunnen maken. Je kan er rechts 1 toevoegen of er eentje bovenop zetten: er zijn dus 2 tromino’s
- Bij de eerste tromino kan je nu een vierkantje bijvoegen rechts, links boven of midden boven. Bij de tweede tromino kan je dat rechts of links van het bovenste vierkantje doen. Zo bekom je 5 tetromino’s ( ook quatromino’s genoemd). Deze figuren kom je tegen bij het spel Tetris.
- Van de blauwe tetromino kan je 3 pentomino’s ( of quintomino’s) maken. Van de oranje kan je dat op 7 manieren doen. Voor de paarse en de groen elk op 1 manier . Je vindt dus 12 pentomino’s.
- Vertrekkend van de pentomino’s ( eerst de bovenste rij van links naar rechts) kan je dan 6 + 4 +11 + 9 + 6 + 9 + 9 + 10 + 5 + 2 + 10 + 5 = 86 figuren maken. Maar sommige zijn hetzelfde, ze kunnen door een rotatie of spiegeling op elkaar worden afgebeeld. er blijven uiteindelijk 35 hexomino’s over :
- Slechts 11 daarvan kunnen een kubus vormen:
7 bruggen van Koningsbergen
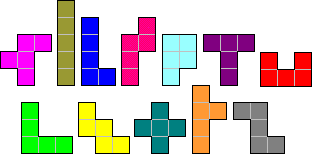
De grote wis- en natuurkundige Leonhard Euler (1707-1783) publiceerde
in 1736 het zogenaamde Koningsberger bruggenprobleem. De stad Koningsbergen, die sinds 1945 Kaliningrad heet, ligt aan de oevers van en op twee eilanden in de rivier de Pregel. De oevers en de eilanden waren in Eulers tijd verbonden door zeven bruggen. De Koningsbergers waren gewend ’s zondags een lange wandeling door de stad te maken en Euler vroeg zich nu af of hij een wandeling zou kunnen ontwerpen, waarbij elk der bruggen juist eenmaal zou gepasserd worden.
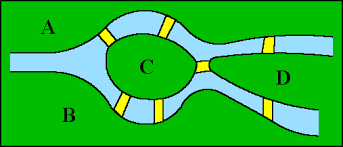
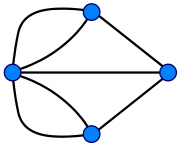
We vereenvoudigen de plattegrond van Koningsbergen door elk der vier stadsdelen A, B, C en D door een punt voor te stellen en elk der zeven bruggen door een lijn. Een dergelijke figuur noemt men een graaf. De graaf in ons probleem heeft vier hoekpunten en zeven kanten. We kunnen het bruggenprobleem nu zo formuleren: Is het mogelijk de graaf zo te doorlopen, dat daarbij elk der kanten slechts éénmaal gepasseerd wordt? Beginnen we bijv. bij het hoekpunt A, dan moet daar een ,,uitgaande kant”, maar ook een ,,inkomende kant” zijn. Telkens als we via een der kanten in een hoekpunt aankomen, moet daar weer behalve de ,,inkomende” ook een ,,uitgaande kant” zijn. Hieruit blijkt, dat als we de graaf zo willen doorlopen, dat we elk der kanten slechts eenmaal gebruiken, er bij elk hoekpunt een even aantal kanten moeten samenkomen. Aangezien dat niet het geval is, is het onmogelijk een wandeling door Koningsbergen te organiseren, waarbij elk der bruggen slechts éénmaal doorlopen wordt.
