Gegeven is een rij van  verschillende getallen. Hieruit kan je zeker ofwel een momotoon dalende ofwel een monotoon stijgende deelrij van
verschillende getallen. Hieruit kan je zeker ofwel een momotoon dalende ofwel een monotoon stijgende deelrij van  elementen kiezen.
elementen kiezen.


Bekijken we een eenvoudig voorbeeld met  . We hebben dus een rij van 10 verschillende getallen en we moeten een monotoon dalende of monotoon stijgende deelrij vinden van 4 elementen. In 2,6,13,4,8,7,3,50,25,10 zit de deelrij 2,6,8,50 die monotoon stijgend is. Met een rij van 9 elementen lukt het niet om een monotoon dalende of monotoon stijgende deelrij te vinden van 4 elementen. Neem bijvoorbeeld 7,8,9,4,5,6,1,2,3.
. We hebben dus een rij van 10 verschillende getallen en we moeten een monotoon dalende of monotoon stijgende deelrij vinden van 4 elementen. In 2,6,13,4,8,7,3,50,25,10 zit de deelrij 2,6,8,50 die monotoon stijgend is. Met een rij van 9 elementen lukt het niet om een monotoon dalende of monotoon stijgende deelrij te vinden van 4 elementen. Neem bijvoorbeeld 7,8,9,4,5,6,1,2,3.
Als we de positie van een element in de rij als x-coördinaat en het element van de rij als y-coördinaat gebruiken kunnen we aan de stelling een meetkundige interpretatie geven: zo er is bijvoorbeeld een pad met 4 stijgende verbindingslijnen te vinden bij 17 gegeven punten:

![]() is een rij van een getallen zodat het quotiënt van twee opeenvolgende termen van die rij constant is. Deze constante noemt men de reden
is een rij van een getallen zodat het quotiënt van twee opeenvolgende termen van die rij constant is. Deze constante noemt men de reden![]() van de rij
van de rij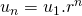

![Rendered by QuickLaTeX.com \[S_n=u_1.\dfrac{1-r^n}{1-r}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-bfd4628b3382cc5011e58c45d998d3ae_l3.png?media=1678572382)
 convergeert als
convergeert als  . In dat geval is de som van de reeks gelijk aan
. In dat geval is de som van de reeks gelijk aan
![Rendered by QuickLaTeX.com \[S=\dfrac{u_1 }{1-r}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-465596c25db0d22501242612fca2aa5a_l3.png?media=1678572382)





