Raadsel

Geplaatst op 1 juli 2020 door admin

De leraar wiskunde stelt volgende vraag op het proefwerk aan zijn leerlingen: ‘Zoek het getal dat ik in gedachten heb. Het getal is gelegen tussen 13 en 1300. En jullie mogen drie vragen stellen over dit getal, waar ik met ja of nee op antwoord, en dan moeten jullie dit getal kunnen bepalen.’

Eerste vraag van de leerlingen: ‘Is het getal kleiner dan 500?’

De leraar antwoordt, maar hij liegt.

Tweede vraag van de leerlingen: ‘Is het getal een volkomen kwadraat?’

De leraar antwoordt, maar hij liegt weer.

Derde vraag van de leerlingen: ‘Is het getal een volkomen derdemacht?’

De leraar antwoordt en nu spreekt hij de waarheid.

De leerlingen beginnen nu te rekenen, maar ze zitten nog vast.

De leraar staat hen dan toe nog een vierde vraag te stellen.

Vierde vraag: ‘Is het laatste cijfer van dat getal een 2?’

De leraar antwoordt en spreekt weer de waarheid.

Eén van de leerlingen heeft het nu gevonden. ‘Dit is het getal’, zegt hij. Het is natuurlijk verkeerd.

Welk is het getal dat de leraar in gedachten had?

Antwoord

Het is duidelijk dat na de derde vraag de leerling nog twee mogelijke getallen in zijn hoofd heeft.
We schrijven alle kwadraten tussen 13 en 1300 ( 16 tot en met 1296) op en ook alle derdemachten ( 27 tot en met 1000)
Er zijn 8 mogelijke scenario’s voor de mogelijke antwoorden van de leraar. JJJ , JNJ,… ( J voor ja en N voor neen)
Stel dat de leerling 3 maal ja krijgt als antwoord, dan vind je alle getallen kleiner dan 500 die zowel een kwadraat als een derde macht zijn, dan krijg je maar 1 oplossing , namelijk 64. dat kan dus niet.
Stel dat je JNN krijgt: kleiner dan 500 en geen kwadraat en geen derde macht: heel veel oplossingen: kan ook niet.
JJN,JNJ,NJJ,NNN en NJN kunnen ook niet .
Wat met NNJ : groter dan 500, geen kwadraat, maar wel een volkomen derde macht: 512 en 1000. Dus twee mogelijkheden.
Maar de leraar liegt bij de twee eerste vragen , dus NNJ wordt JJJ en dan is er maar 1 oplossing ,namelijk 64

Een touw rond de aarde

Geplaatst op 16 juni 2020 door admin

Neem een touw dat strak gespannen is rond een voetbal. Hoeveel langer moet ik dat touw maken om het 10 cm boven het oppervlak van de voetbal te laten lopen? Span vervolgens een touw om de evenaar. Dat zou 40000 km lang zijn. Hoeveel langer moet dit touw zijn om het rondom 10 cm te laten lopen?

Eenvoudige wiskunde kan ons helpen om onze intuïtie te overstijgen. De meesten onder ons denken inderdaad dat de oplossing bij het touw rond de evenaar veel langer is dan bij de voetbal. Mis!

Als R de straal is van de bal dan is de lengte van ons touw $2\pi R$ en na de vergroting $2\pi(R+0,10)$ meter. Hieruit blijkt dat het verschil $2\pi \times 0,10$ meter is, ongeacht de straal van de voetbal of aarde. Bij benadering is dat 62,83 cm.

Dit vraagstuk komt uit een werk van William Whiston, een Engelse wiskundige en theoloog(1667 – 1752), voor zijn studenten schreef: De elementen van Euclides (1702). Hij was een leerling van Newton en volgde hem op als professor aan de universiteit van Cambridge. In 1710 werd hij er ontslagen wegens zijn onorthodoxe religieuze inzichten. Hij vond het, onder andere, een belediging van God, om te geloven in het vuur van de hel.

Magische driehoek

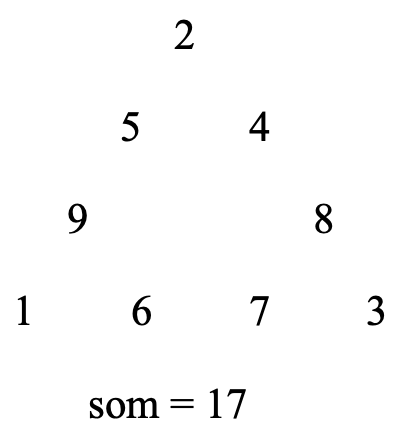
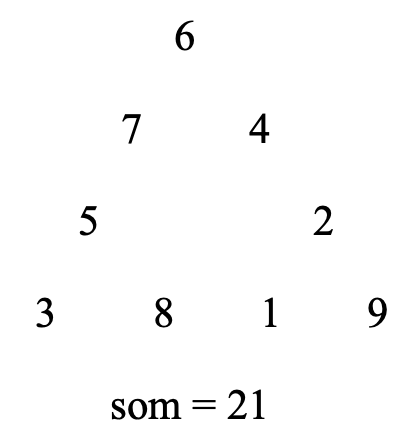
Geplaatst op 29 april 2020 door admin

Plaats de cijfers van 1 tot en met 9 in de cirkeltjes in het diagram zodat de som van de vier cijfers langs de drie zijden gelijk is aan 17. En hoe kan je ze rangschikken zodat de som langs de drie zijden telkens gelijk is aan 20? Is er een andere som mogelijk?

Deze puzzel komt uit het boek The Moscow puzzels van Boris Kordemsky(1907-1999), een wiskundedocent uit Moskou.

Spoiler

Noteer de som langs de drie zijden door x en de som van de elementen in de hoekpunten door s.
de som van alle cijfers 1 tot 9 is 45.
Dus 45=3x – s. Hieruit volgt dat s een drievoud moet zijn.
Voor x = 17 vinden we s = 6 en krijgen we volgende oplossing:
voor x = 20 vinden we s= 15 en vinden we de oplossingen:
We vinden ook een oplossing voor x = 21 met s = 18:
Andere oplossingen hebben we niet gevonden.

De drie snelste paarden

Geplaatst op 23 maart 2020 door admin

De eigenaar van een mooie renstal met 25 paarden wil uitzoeken welke drie paarden het snelst zijn. Hij kan dit echter alleen doen door de paarden tegen elkaar te laten lopen. Maar hij kan slechts vijf paarden tegelijkertijd laten lopen. Hoeveel races heb je minimaal nodig om de drie snelste paarden te selecteren.

Verdeel de 25 paarden in 5 groepjes van 5 en duid in elke groep het snelste paard aan door 5 races te organiseren. Laat in de zesde wedstrijd de 5 winnaars tegen elkaar uitkomen. Zo kan het allersnelste paard worden aangeduid in 6 races.
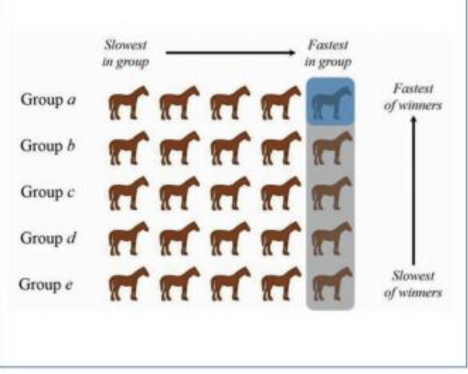
Om het tweede en derde snelste paard aan te duiden heb je maar 1 extra wedstrijd nodig:

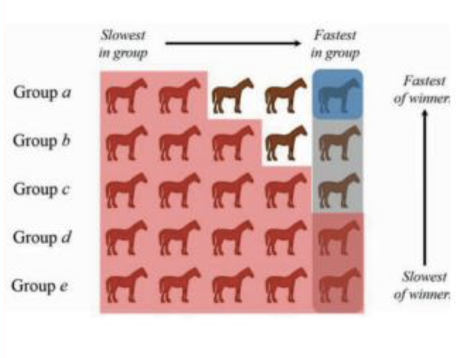
In de tekening hierboven staan de paarden per groep, van links naar rechts, in volgorde van snelheid. de traagste helemaal links. De groepen zelf zijn gerangschikt van onder naar boven volgens de snelheid van hun winnaar; de traagste helemaal onderaan. In het rood zijn alle paarden aangeduid waarvan we weten dat er nog minstens drie snellere paarden zijn. Er blijven nog zes paarden over. Het paard rechtsboven is de allersnelste en laten we even buiten beschouwing. Laat de vijf andere tegen elkaar lopen in de zevende race. Zo vinden we de zilveren en bronzen medaille!

Verwarring

Geplaatst op 7 oktober 2019 door admin

Drie vrienden zitten op een terrasje en de ober brengt de rekening van 30 euro. Ze geven elk 10 Euro. De ober brengt het geld naar zijn baas, maar die ziet dat er een vergissing is gebeurd. Er is 5 Euro te veel gevraagd en hij zegt aan de ober het geld terug te geven aan de 3 vrienden. De ober steekt echter 2 Euro in zijn zak en geeft elk van de 3 vrienden 1 Euro terug.

Raar, want ze hebben nu elk 9 Euro betaald en samen met de 2 Euro die de ober op zak stak kom je uit op 3×9+2 = 29 Euro. Waar is de laatste Euro naar toe?