Je hebt 10 stapels van 10 munten. Elke munt van 9 van die stapels weegt 6 gram? Maar de munten van de 10de stapel wegen elk maar 5 gram. Hoe kan je met slechts 1 weging weten in welke stapel de munten van 5 gram zitten?
Antwoord
Categorie archieven: Raadsels/spelen
Pig
Een speler werpt met een dobbelsteen tot er een 1 is gegooid of de speler zijn beurt opgeeft en het totaal aantal ogen van die beurt als winstpunten noteert. Wie het eerst 100 punten of meer scoort is de winnaar.
Voorbeeld: speler A gooit een 6 , dan een 4 en dan een 1: geen punten en de beurt gaat naar speler B. Die gooit een 3,4 en een 6 en besluit het hierbij te laten. Hij noteert 13 punten en de beurt is terug bij A.
Dit spel, Pig genoemd, werd voor het eerst beschreven in 1945 door de Amerikaanse goochelaar John Scarne. Het is een afwegingsspel: na elke worp van iets anders dan 1 moet worden beslist of de kans op meer punten opweegt tegen de kans om een 1 te gooien en alle punten van de beurt te verliezen.
Is er winnende strategie?Enkele computerwetenschappers hebben met behulp van wat wiskunde en computergraphics een winnende strategie gevonden. Als beide spelers nog een lage score hebben, dan kan je die benaderen door te stoppen éénmaal je 20 of meer. scoort bij je beurt . Bij iets hogere totalen kan je beter stoppen eens je 25 of meer hebt en als je al meer dan 70 punten hebt, dan ga je gewoon voor een zo hoog mogelijke beurt.
Icosian
Het spel icosian heeft als doel een route te vinden langs de ribben van een twaalfvlak zodat elk hoekpunt slechts één keer wordt aangedaan. Het spel werd beschreven door de Ierse wiskundige William Hamilton(1805-1865).
In de moderne grafentheorie zoeken we naar een rondgang waarbij elk hoekpunt van de graaf één keer wordt aangedaan. Een hamiltonpad is een route die eindigt bij het beginpunt.
Haberdasher puzzel
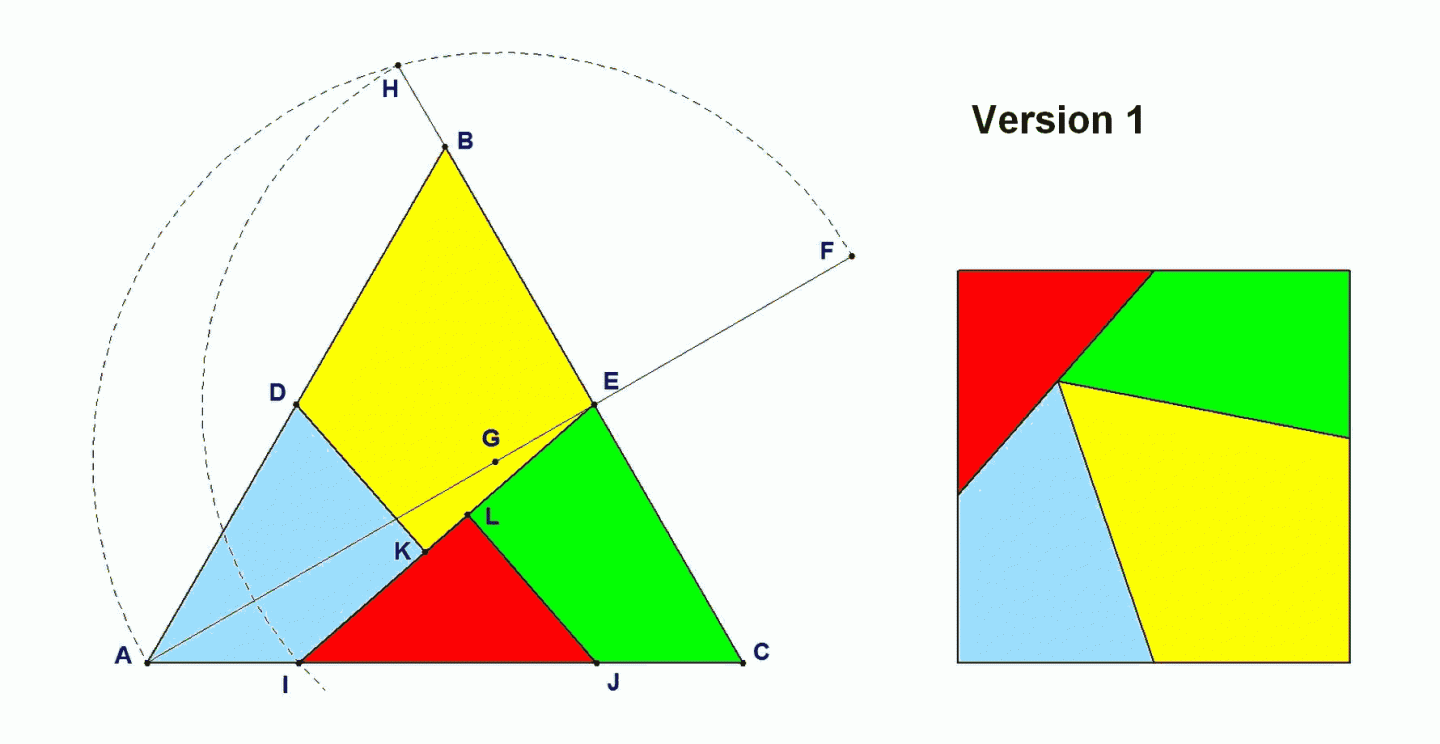
In 1907 werd een bundeling van meer dan 100 puzzelproblemen gepubliceerd in het boek Canterbury puzzels van Henry Dudeney (1857 – 1930 . Dudeney was een Engels auteur en wiskundige met een voorliefde voor logische puzzels en wiskundige spelletjes. Eén van de meest bekende puzzels is de volgende: gegeven is een gelijkzijdige driehoek. Maak met slechts 3 insnijdingen van de driehoek 4 puzzelstukjes die kunnen omgevormd worden tot een vierkant met dezelfde oppervlakte als de gegeven driehoek.
Een mogelijke oplossing wordt gegeven als volgt:
- Het midden van AB is D en van BC is het E.
- Verleng AE to F zodat EF=EB.
- G is het midden van AF.
- Met G als middelpunt beschrijven we de boog AHF, waarbij H gelegen is op het verlengde van EB
- Met E als middelpunt tekenen we de boog HI.
- Construeer J op AC zodat IJ=BE
- Teken IE
- Teken uit D en J de loodlijnen op IE met voetpunten K and L.
Een alien
Op het bord staat de vergelijking
![\[x^3-19x^2+103x-247=0\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-100b7069aebfa55d41a60aacb442b71c_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
Een alien komt binnen en roept: een drievoudige wortel! Net als wij heeft het buitenaards wezen 2 handen die onderling symmetrisch zijn. maar hoeveel vingers heeft hij (zij of het) aan elke hand?
antwoord
of ![\[x^3-3kx^2+3k^2x-k^3=0\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-be161a9126b391526c8e1efc90e04571_l3.png?media=1678572382 "Rendered by QuickLaTeX.com")
of 
. Hieruit volgt dat 
.
of 
. Als we hierin k vervangen door 
vinden we 
. Bijgevolg is k=12 of k=-3. Dit laatste kan uiteraard niet.
met b=12. Dit klopt.