Toon aan dat volgende veeltermfunctie nooit de getalwaarde 33 aanneemt voor willekeurige gehele waarden van x en y.
![]()
Antwoord
Antwoord
- We moeten bewijzen dat de vergelijking
![Rendered by QuickLaTeX.com \[x^5+3x^4y-5x^3y^2-15x^2y^3+4xy^4+12y^5 =33\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-85e78187ff0ebf243f9433664d1c85c4_l3.png?media=1678572382)
geen oplossingen heeft voor gehele waarden van x en y. We stellen onmiddellijk vast dat x en y zeker verschillend van nul moeten zijn.
- Er bestaan geen algemene methoden om een vijfde graads vergelijking op te lossen. We zouden eventueel
 kunnen proberen te ontbinden in factoren om zo bovenstaande vergelijking op te lossen. Maar dit lukt niet.
kunnen proberen te ontbinden in factoren om zo bovenstaande vergelijking op te lossen. Maar dit lukt niet. - Maar de uitdrukking
 kunnen we wel ontbinden als
kunnen we wel ontbinden als
![Rendered by QuickLaTeX.com \[(x-2y)(x-y)(x+y)(x+2y)(x+3y)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-a3fdfad834561ef0b6f4372b46bd5ef3_l3.png?media=1678572382)
- Het probleem wordt dus herleid tot : bewijs dat
 geen oplossingen heeft voor gehele waarden van x en y.
geen oplossingen heeft voor gehele waarden van x en y. - Nu heeft 33 als delers
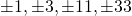 . We kunnen 33 dus hoogstens schrijven als het product van 4 verschillende gehele getallen ( vier positieve ofwel 2 negatieve en 2 positieve). Omdat x en y geheel moeten zijn is het linkerlid van vorige vergelijking steeds het product van 5 verschillende gehele getallen.
. We kunnen 33 dus hoogstens schrijven als het product van 4 verschillende gehele getallen ( vier positieve ofwel 2 negatieve en 2 positieve). Omdat x en y geheel moeten zijn is het linkerlid van vorige vergelijking steeds het product van 5 verschillende gehele getallen. - Bijgevolg heeft de vorige vergelijking geen oplossingen voor gehele waarden van x en y.

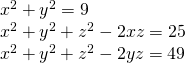
![Rendered by QuickLaTeX.com \[n=\sum_{i=0}^hn_i.2^{h-i}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-0a461b163b130555b12f5672bfe5a547_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[s=\sum_i^ps_i.2^{p-i}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ba1bb5df96b961585aeab0256809b2c5_l3.png?media=1678572382)