Uit {1,2,…,n} worden 4 opeenvolgende even getallen verwijderd. De overgebleven getallen hebben een gemiddelde van 51+ 9/16. Bepaal alle viertallen opeenvolgende even getallen die hieraan voldoen.
Antwoord
Antwoord
- Stel die 4 opeenvolgende getallen voor door 2k, 2k+2, 2k+4 en 2k+6.
- De som van d eandere getallen is dan
 .
. - Het gemiddelde is dan
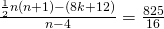 .
. - Hieruit volgt dat
 .
. - 8 is een deler van het rechterlid en dus ook van het linkerlid. Bijgevolg bestaat er een geheel getal m waarvoor
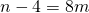 . Ingevuld in vorige vergelijking vinden we dan dat
. Ingevuld in vorige vergelijking vinden we dan dat 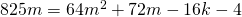 .
. - 4 deelt het rechterlid en dus ook het linkerlid, dus bestaat er een geheel getal l zodat
 . Invullen geeft dan
. Invullen geeft dan 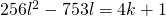 .
. - Nu is
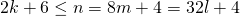 . Bijgevolg is
. Bijgevolg is  en dus ook
en dus ook 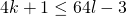 .
. - Uit vorige twee punten volgt dan dat
 of
of
![Rendered by QuickLaTeX.com \[256l^2-817l+3\leq 0\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-ad8a384ac9132ab072ae5f9c520281cf_l3.png?media=1678572382)
- Enkel
 voldoen en omdat
voldoen en omdat 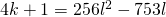 , zal uiteindelijk enkel
, zal uiteindelijk enkel 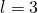 een oplossing geven voor k, namelijk
een oplossing geven voor k, namelijk  .
. - De 4 gezochte getallen zijn dan 22, 24, 26 en 28.
