Opgave 37

Geplaatst op 30 juli 2023 door admin

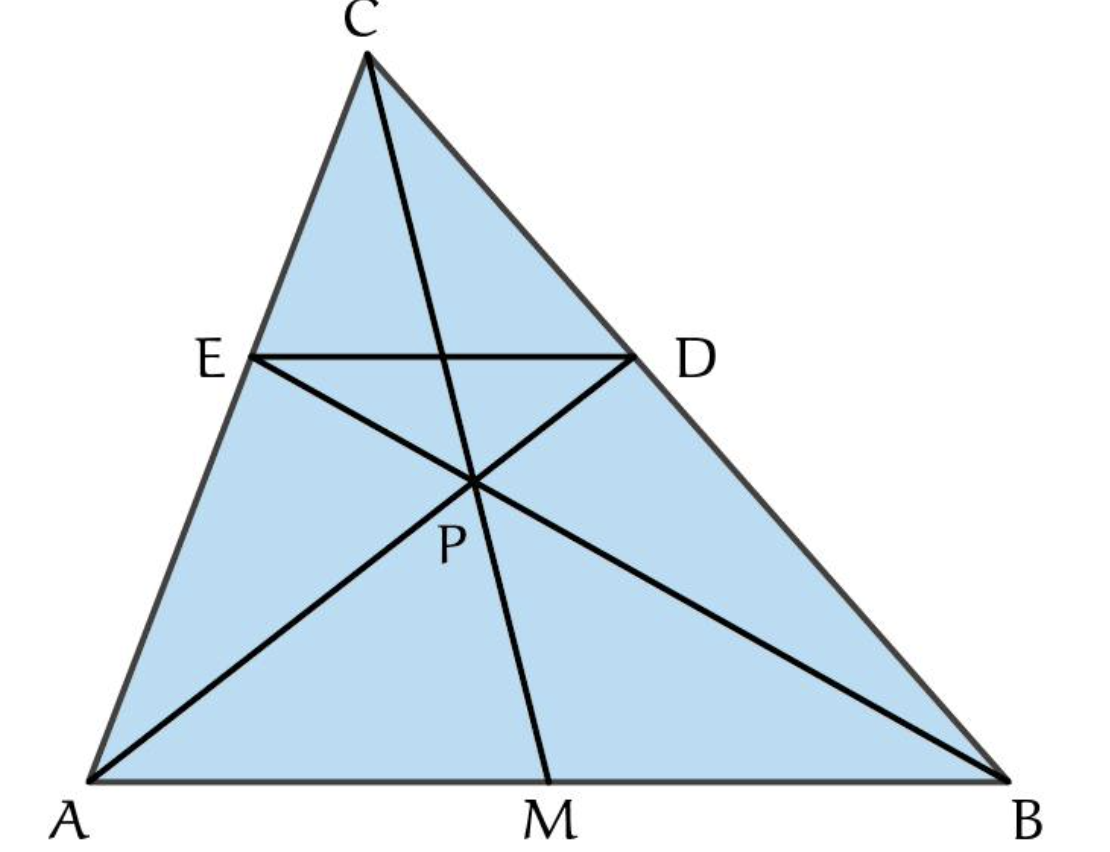
Neem een willekeurig punt P op de zwaartelijn CM, construeer PA en PB met respectievelijke snijpunten D en E. Bewijs dat ED evenwijdig is met AB.

We gebruiken eerst de stelling van Ceva:
$\frac{|AM|}{|MB|}.\frac{|BD|}{|DC|}.\frac{|CE|}{|EA|}=1$
Omdat M het midden is volgt hieruit dat
$\frac{|BD|}{|DC|}.\frac{|CE|}{|EA|}=1$
Volgens de omgekeerde stelling van Thales is dan ook ED evenwijdig met AB

Opgave 36

Geplaatst op 26 september 2022 door admin

Wanneer deelt een natuurlijk getal n de uitdrukking $10^k-1$ voor een natuurlijke k?

Spoiler

Opgave 35

Geplaatst op 14 september 2022 door admin

N is een natuurlijk getal. Een goede verdeling van N is een partitie van $\{1,2,\cdots,N\}$ in twee gescheiden, niet lege deelverzamelingen $S_1$ en $S_2$ , zo dat de som van de elementen van $S_1$ gelijk is aan het product van de elementen van $S_2$ . Bewijs dat voor $N\geq 5$ er altijd een goede verdeling bestaat.

Spoiler

Opgave 34: Een integraal…

Geplaatst op 4 maart 2022 door admin

Bereken $A=\int_0^{\frac{\pi}{4}} ln(1+tan x) dx$

Gewone methoden werken hier niet.
Als een functie f gedefinieerd is op $\left[a,b\right]$ dan kan je de functie spiegelen rond de middelloodlijn van dit lijnstuk en bekom je de functie $g(x)=f(a+b-x)$ .
Uit de definitie van de bepaalde integraal volgt dan dat $\int_a^bf(x) dx=\int_a^b g(x) dx$ .
Passen we dit toe op de opgave , dan krijgen we: $A=\int _0^{\frac{\pi}{4}} ln(1+tan(\frac{\pi}{4}-x)) dx$ .
Nu is $tan(\frac{\pi}{4}-x)=\frac{1-tan x}{1+tan x}$ .
Zodat $A=\int _0^{\frac{\pi}{4}} ln\Big( \frac{2}{1+ tan x}\Big) dx$ .
Gebruikmakend van de rekenregels voor logaritmen, volgt hieruit dat $A=\int _0^{\frac{\pi}{4}} ln(2) dx -A$ .
Bijgevolg is $A=\frac{\pi}{8} ln(2)$ .