Categorie archieven: Ongelijkheden

Ravi substitutie

Geplaatst op door

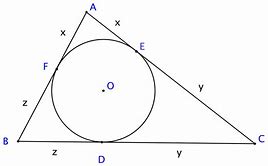
De Ravi substitutie is een techniek die erg belangrijk is bij het oplossen van meetkundige ongelijkheden. Ze luidt als volgt:

Als a, b en c zijden van een driehoek zijn dan bestaan er positieve getallen x,y en z zodat 

    \[a = y + z, b = z + x \text{ en } z = x + y\]

Het bewijs hiervan is niet zo lastig. Als a ,b en c zijden zijn van een driehoek, dan kunnen we de ingeschreven cirkel tekenen en uit onderstaande tekening volgt het gestelde.

Omgekeerd, zijn a, b en c de zijden van een driehoek als elke zijde kleiner is dan de som van de twee andere zijden. En dat is evident omdat x,y en z positief zijn.

Voorbeeld: Als a, b en c de zijden van een driehoek zijn bewijs dan dat

    \[abc \geq (b+c-a)(c+a-b)(a+b-c)\]

We gebruiken de Ravi substitutie en we moeten dan bewijzen dat :

    \[(y+z)(z+x)(x+y)\geq xyz\]

  of

    \[x(y-z)^2+y(z-x)^2+z(x-y)^2\geq 0\]

Omdat x,y en z positief zijn is dit correct.

De naam Ravi substitutie komt van de Canadese wiskundige Ravi D. Vakil, (geboren in 1970) die deze reeds gekende substitutie als één van zijn favoriete methodes gebruikte bij het oplossen van ongelijkheden. Hij was lid van het Canadese team bij de Internationale Wiskunde Olympiade in 1986,1987 en 1988 en behaalde zilver en twee maal goud (éénmaal met een perfecte score).

Nog een goniometrische ongelijkheid

Geplaatst op door

In een driehoek met hoeken \alpha,\beta en \gamma geldt:

    \[\cot \alpha.\cot \beta.\cot \gamma \leq \frac{\sqrt{3}}{9}\]

  • Als één van de hoeken groter is dan 90^{\circ} dan is de cotangens ervan negatief en klopt de eigenschap zeker.
  • Veronderstel dus dat alle hoeken scherp zijn, dan is de tangens functie convex en volgt uit de stelling van Jensen dat:  \tan \alpha +\tan \beta +\tan \gamma \geq 3\tan(\frac{\alpha+\beta+\gamma}{3})=3\sqrt{3}.
  • Men kan eenvoudig controleren dat \tan \alpha +\tan \beta +\tan \gamma =\tan \alpha .\tan \beta .\tan \gamma en dus is  \tan \alpha .\tan \beta .\tan \gamma \geq 3\sqrt{3}.
  • Als we het omgekeerde nemen vinden we dat  \cot \alpha .\cot \beta .\cot \gamma \leq \frac{1}{ 3\sqrt{3}}=\frac{\sqrt{3}}{9}.

Ongelijkheid met sinussen

Geplaatst op door

Sommige ongelijkheden kunnen zeer elegant worden opgelost door gebruik te maken van de ongelijkheid van Jensen. Voor concave functies ( bol , tweede afgeleide negatief) wordt dit :

    \[\frac{f(x)+f(y)+f(z)}{3} \leq f\Big( \frac{x+y+z}{3}\Big)\]

In een driehoek met hoeken \alpha,\beta en \gamma geldt :

    \[\sin \alpha +\sin \beta +\sin \gamma \leq \ \frac{3\sqrt{3}}{2}\]

Omdat \alpha,\beta,\gamma hoeken zijn van een driehoek zijn \alpha,\beta,\gamma elementen van [0,\pi ]. De sinusfunctie is concaaf op dit interval, want \sin''(x)=-\sin x \leq 0 in [0,\pi ]. Dus is, volgens Jensen: \frac{\sin \alpha+\sin \beta +\sin \gamma}{3}\leq \sin \frac{\alpha+\beta+\gamma}{3}=\sin \frac{\pi}{3} =\frac{\sqrt{3}}{2}.

Dus is \sin \alpha+\sin \beta +\sin \gamma} \leq \frac{3\sqrt{3}}{2}.

Ongelijkheid van Jensen

Geplaatst op door

Voor elke functie f waarvan de grafiek ‘hol’ naar onder is , of dus convex (d.w.z dat het verbindingstuk van twee punten van de grafiek altijd boven de grafiek ligt ) geldt volgende ongelijkheid:

    \[f(\dfrac{a_1+a_2+\cdots+\a_n}{n} )\leq \dfrac{f(a_1)+f(a_2)+\cdots+f(a_n)}{n}\]

Deze ongelijkheid staat bekend als de ongelijkheid van Jensen, naar de Deense wiskundige Johan Willem Ludwig Valdemar Jensen (1859-1925).

Uiteraard is er een analoge formule voor concave functies.

Voorbeeld: Als a,b en c positieve hoeken zijn met een som gelijk aan \frac{\pi}{2}, dan is \tan a+ \tan b+\tan c \geq \sqrt{3}.

Tussen 0 en \frac{\pi}{2} is de tangensfunctie convex, dus geldt er volgens Jensen dat \tan (\dfrac{a+b+c}{3}) \leq \frac{1}{3}( \tan a+\tan b+\tan c). Hieruit volgt dat \frac{1}{3}( \tan a+\tan b+\tan c) \geq \tan(\frac{\pi}{6})=\frac{\sqrt{3}}{3}. Vermenigvuldigen met 3 geeft het gevraagde antwoord.

 

Eenvoudige ongelijkheden

Geplaatst op door

Het is voor iedereen duidelijk dat een kwadraat van een reeël getal nooit negatief kan zijn. Het uitwerken van (a-b)^2\geq 0 geeft ons twee eenvoudige ongelijkheden, waarmee we snel aan het werk kunnen ( veronderstel alle getallen positief):

  • \sqrt{ab} \leq \frac{a+b}{2}.
  • \Big(\frac{a+b}{2}\Big)^2 \leq \frac{a^2+b^2}{2}.

Twee voorbeelden:

  1. Bewijs dat (a+b)(b+c)(c+a)\geq 8abc.

    Uit formule 1  vinden we a+b \geq 2\sqrt{ab}, maar ook dat a+c \geq 2\sqrt{ac} en c+b \geq 2\sqrt{cb}, dus is (a+b)(b+c)(c+a)\geq 8\sqrt{ab}\sqrt{bc}\sqrt{ca}=8abc.
  2. Bewijs, als a+b=1, dan is \Big(a+\frac{1}{a}\Big)^2+\Big(b+\frac{1}{b}\Big)^2 \geq \frac{25}{2}.
    Uit formule 2 volgt het linkerlid groter is dan of gelijk is aan \frac{2}{4}\Big(a+\frac{1}{a}+b+\frac{1}{b}\Big)^2=\frac{1}{2}\Big(1+\frac{a+b}{ab}\Big)^2 =\frac{1}{2}\Big(1+\frac{1}{ab}\Big)^2.  Uit formule 1 weten we dat a+b=1 \geq 2\sqrt{ab} ofwel ab \leq \frac{1}{4}. Hieruit volgt dat \frac{1}{ab} \geq 4.
    Bijgevolg is \Big(a+\frac{1}{a}\Big)^2+\Big(b+\frac{1}{b}\Big)^2 \geq \frac{1}{2}(1+4)^2=\frac{25}{2}.