Categorie archieven: Meetkunde

Het probleem van Fagnano

Geplaatst op door

Gegeven is een scherphoekige driehoek ABC. Zoek een ingeschreven driehoek DEF  met de kleinst mogelijke omtrek.

Dit probleem werd in 1775 gesteld door de Italiaanse wiskundige J.F.Fagnano.

Eén van heuristieken gebruikt bij problem solving leert ons het probleem aan te pakken voor een speciaal geval: neem het  punt D  vast. Spiegel vervolgens D rond de twee aanliggende zijden tot S en T.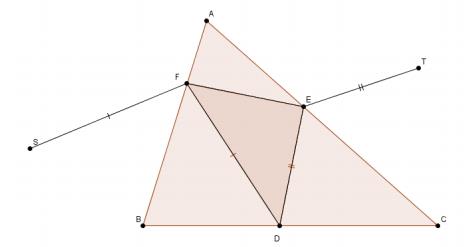 

De omtrek van DEF is gelijk aan de lengte van SFET. De kleinst mogelijke omtrek krijgen we dus als als SFET zo klein mogelijk is, dus als we F en E nemen op de rechte ST.
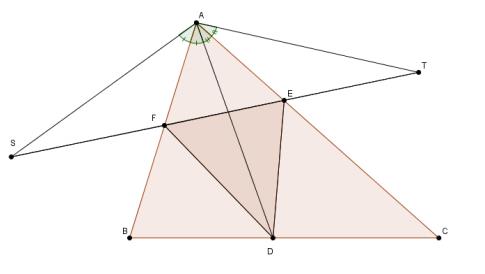Merk op dat de driehoek SAT gelijkbenig is en dat de tophoek SAT gelijk is aan het dubbele van de hoek BAC. Aangezien het lijnstuk [ST] de basis is van een gelijkbenige driehoek met een vaste tophoek, zal deze basis zo klein mogelijk zijn als de lengte van de benen [AS] en [AT] zo klein
mogelijk is. We moeten het punt D dus zo kiezen dat [AS] en [AT] zo klein mogelijk zijn. Het is duidelijk dat |AS| = |AD| = |AT|. We moeten dus D op [BC] kiezen zodat|AD| zo klein mogelijk is. Bijgevolg moet D het voetpunt zijn van de loodlijn uit A op [BC] . 

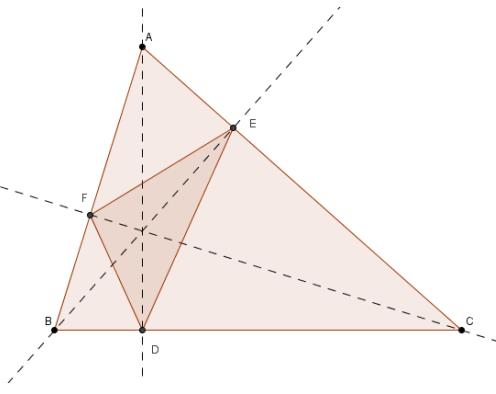
Natuurlijk kunnen we in plaats van met D te beginnen ook via E of F werken. Zo krijgen we als oplossing de voetpuntsdriehoek:

 

 

Formules in een driehoek

Geplaatst op door

We geven 7 eigenschappen die, bij het onderzoeken van eigenschappen van een driehoek, zeer nuttig kunnen zijn. Noteer de halve omtrek van de driehoek met s en de oppervlakte met K. Verder zijn r en R respectievelijk de stralen van de ingeschreven en omgeschreven cirkel.

  • K=\frac{1}{2}ab \sin \gamma=\frac{1}{2}ac \sin \beta=\frac{1}{2}bc\sin \alpha.
  • K=\sqrt{s(s-a)(s-b)(s-c)}. (formule van Heroon)
  • K=rs.
  • 2R=\frac{a}{\sin \alpha}=\frac{b}{\sin \beta}=\frac{c}{\sin \gamma}.(sinusregel)
  • K=\frac{abc}{4R}.
  • 1+\cos \alpha=\frac{(a+b+c)(-a+b+c)}{2bc},1-\cos \alpha=\frac{(a-b+c)(a+b-c)}{2bc}.
  • \sin \frac{\alpha}{2}=\sqrt{\frac{(s-b)(s-c)}{bc}},\cos \frac{\alpha}{2}=\sqrt{\frac{s(s-a)}{bc}}.

De ongelijkheid van Euler

Geplaatst op door

Eén van de oudste ongelijkheden in een driehoek is de ongelijkheid van Euler die een verband geeft tussen de stralen van de omgeschreven en ingeschreven cirkel.

Als O het middelpunt is van de omgeschreven cirkel ( met straal R) van driehoek ABC en I het middelpunt van de ingeschreven cirkel (met straal r), noteer dan d=|OI|. Dan geldt er:

    \[d^2=R^2-2Rr\]

Hieruit volgt dan dat

    \[R\geq 2r\]

Het gelijkheidsteken geldt enkel als de driehoek gelijkzijdig is.

Lengte zwaartelijn en bissectrice

Geplaatst op door

Om de lengte van een zwaartelijn te berekenen, gebruiken  we de cosinusregel in de driehoeken ABD en ACD voor b^2 en c^2. Optellen van de formules geeft:

    \[4z_a^2=2b^2+2c^2-a^2\]

Als a\geq b\geq c dan is z_a \leq z_b\leq z_c. Want 4(z_a^2-z_b^2)=3(b^2-a^2). Dus bij de langste zijde hoort de kortste zwaartelijn.

Het berekenen van de lengte van een bissectrice is heel wat lastiger. Noteer c=|BD| en y=|DC|.

Een bissectrice in een driehoek verdeelt de overstaande zijde in de verhouding van de aanliggende zijdes, dus x:y=c:b. Volgens de eigenschappen van evenredigheden volgt hieruit dat (x+y):y=(c+b):b of y=\frac{ab}{b+c} en analoog x=\frac{ac}{b+c}. Teken nu een punt E zodat de hoek ACE gelijk is aan de hoek ADB. Uit de gelijkvormigheid van de driehoeken ACE en ADB volgt dat |AE|.d_a=bc en uit de gelijkvormigheid van de driehoeken DEC en ABD volgt dat |DE|.d_a=xy. Door die twee formules van elkaar af te trekken vinden we dat:

    \[d_a^2=bc-\frac{a^2bc}{(b+c)^2}\]

Net zoals bij de zwaartelijnen kunnen we besluiten dat bij de langste zijde de kortste bissectrice hoort.

Door gebruik te maken van deze formules kan je door algebraïsche berekeningen meetkundige eigenschappen bewijzen, zoals bijvoorbeeld: De langste bissectrice is minstens even lang als de kortste zwaartelijn. Als a\geq b\geq c dan komt dit neer op d_c \geq z_a.

Een meetkundige plaats

Geplaatst op door

Gegeven is een cirkel met middelpunt A en straal R en een punt B buiten de cirkel. Neem een willekeurig punt Q op die cirkel en bereken het snijpunt P van QA met de middelloodlijn van QB. Bepaal de meetkundige plaats van de punten P als Q zich op d ecirkel beweegt.

  • We schakelen Geogebra in om een inpressie te krijgen van die meetkundige plaats:
  • De oplossing lijkt een hyperbool te zijn. Omdat P op de middelloodlijn van QB ligt is |PQ|=|PB| en bijgevolg is |PA|+R=|PB| of

        \[|PB|-|PA|=R\]

    Het verschil van de afstanden van P tot twee vaste punten A en B is dus constant en daarom is de meetkundige plaats inderdaad een hyperbool.

  • In de tekening zijn ook de raaklijnen uit B aan de cirkel getekent ( met raakpunten D en E). Als Q samenvalt met D of E dan bestaat P niet, omdat QA dan loodrecht staat op QB en dus evenwijdig is met de middelloodlijn.
  • Als Q samenvalt met de snijpunten van AB met de cirkel, dan vinden we de toppen van de hyperbool.
  • Als Q de grote boog DE doorloopt, dan vinden we de linkertak van de hyperbool. Het andere deel van de cirkel coorespondeert dan met de rechtertak.