Categorie archieven: Meetkunde

Een meetkundige parel

Geplaatst op door

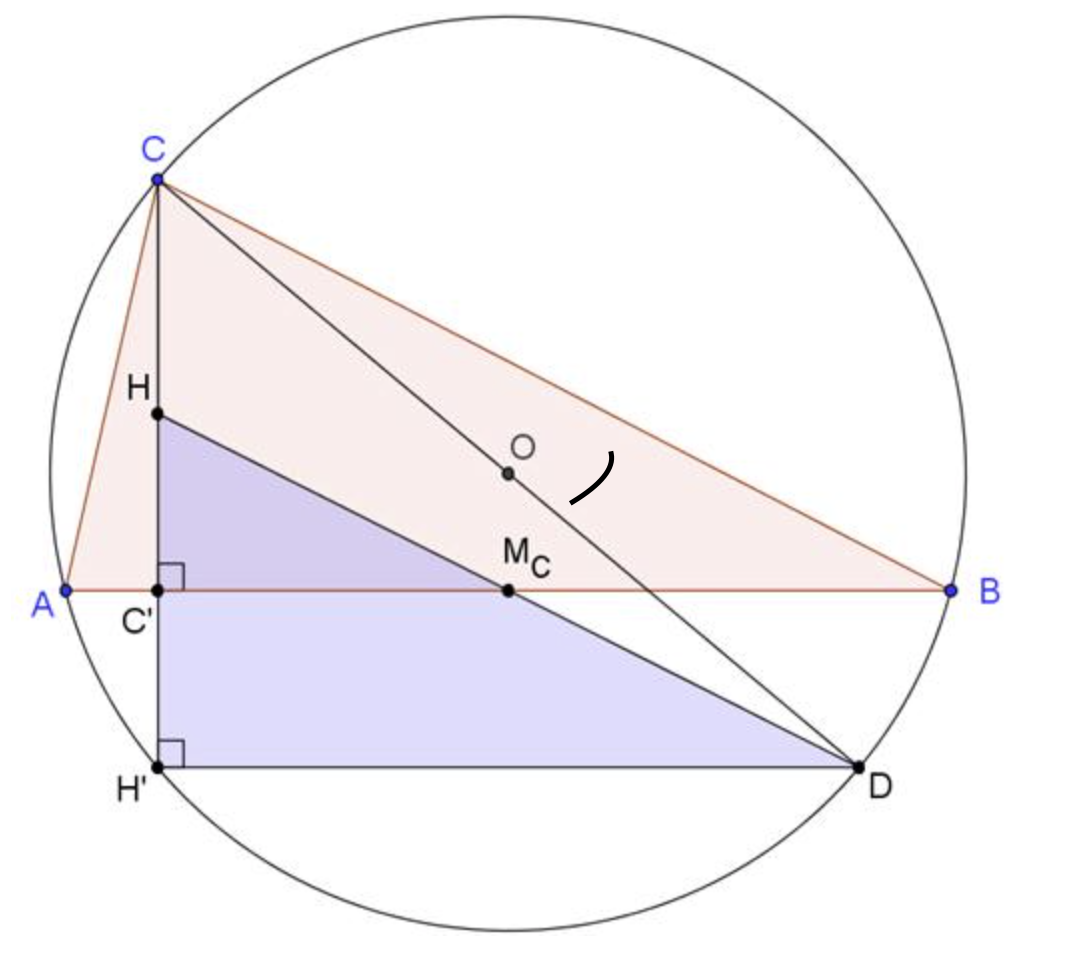
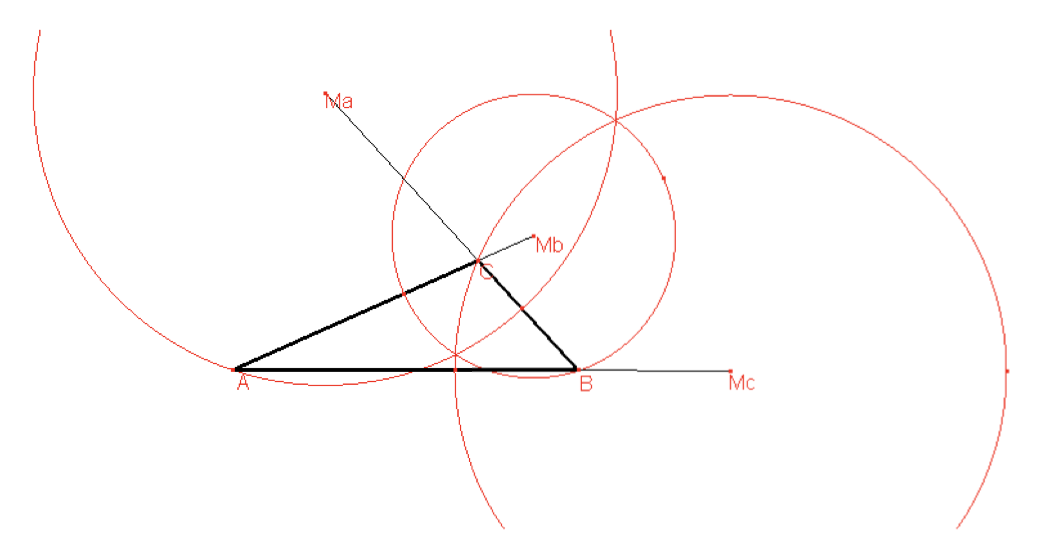
Onlangs vond ik volgende stelling die ik helemaal niet kende. Een echt pareltje: De spiegelbeelden van het hoogtepunt van een driehoek ABC rond de zijden en rond de middens van de zijden liggen op de omgeschreven cirkel van ABC.

H’ is het spiegelbeeld van H (hoogtepunt) rond de zijde AB en CD is een middellijn van de omgeschreven cirkel.

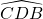  • \widehat{CDB} is een rechte hoek, als omtrekshoek op een halve cirkel. Omdat AH loodrecht op BC staat, zijn BD en AH evenwijdig.
  • Analoog is AD ook evenwijdig met BH.
  • Dus is AHBD een parallellogram. 
  • Omdat de diagonalen van een parallellogram elkaar midden doordelen is 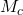M_c het midden van AB en dus is D inderdaad het spiegelbeeld van H bij een puntspiegeling rond het midden van B.
  • Omdat HC’=C’H’ is 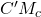C'M_c de middenparallel van driehoek HH’D en staat DH’ loodrecht op CC’ omdat DH’ evenwijdig is met C'M_c.
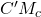  • Dus is 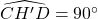\widehat{CH'D}=90^\circ  en wegens de eigenschappen van omtrekshoeken ligt dus H’ op de omgeschreven cirkel van driehoek ABC.

Isogonaal toegevoegde punten

Geplaatst op door

Om het isogonaal toegevoegd punt van P  te berekenen, construeert men het snijpunt van de spiegelbeelden van AP, BP en CP ten opzichte van de respectievelijke bissectrices van de hoeken A,B en C. Het is duidelijk dat de hoeken CAP en  QAB gelijk zijn. analoog zijn ook ABP en QBC gelijk en BCP en QCA.

Een andere mogelijke constructie werkt met de voetpuntsdriehoek:

Men tekent de loodlijnen vanuit P op de drie zijden van de driehoek. Hun voetpunten vormen de voetpuntsdriehoek. Construeer nu snijpunt Q van de loodlijnen uit A,B en C op de zijden van de voetpuntsdriehoek. Dan zijn P en Q isogonaal toegevoegd.

Een paar voorbeelden:

  • Het middelpunt van de ingeschreven cirkel is isogonaal toegevoegd aan zichzelf.
  • Het hoogtepunt van een driehoek en het middelpunt van zijn omgeschreven cirkel zijn isogonaal toegevoegd.

Perfecte rechthoeken

Geplaatst op door

Een rechthoek R die kan verdeeld worden in verschillende vierkanten van verschillende grootte,  noemt men een perfecte rechthoek. Zo een verdeling noemt men vierkansverdeling van orde n als er n verschillende vierkanten gebruikt worden.

Dit is een vierkansverdeling van orde 9 van een rechthoek van 32 bij 33. Deze verdeling werd gevonden door A Moron (1904-1971), een Pools wiskundige in 1925.

Lange tijd dacht men dat perfecte vierkanten niet bestonden.  Tot in 1939 de Duitse wiskundige R. Sprague een perfect vierkant vond van orde 55. Later , in 1940 hebben Reichert en Toepkin zelfs bewezen dat een perfect vierkant van een orde kleiner dan 9 niet bestaat. 

21 is de kleinste orde voor een perfect vierkant. Hieronder zie je een perfect vierkant met een unieke 21 vierkansverdeling . Is de orde hoger dan 21, dan zijn er meerder vierkanten mogelijk; zo zijn er bijvoorbeeld 441 perfecte vierkanten van orde 26.

Stelling van Viviani

Geplaatst op door

Kies een punt binnen een gelijkzijdige driehoek. Bereken de afstand van dit punt tot de drie zijden van de driehoek. Waar je dit punt ook plaatst de som van die afstanden is gelijk aan de hoogte van de driehoek.

De stelling kan eenvoudig bewezen worden. Noem het punt P en de driehoek ABC. De oppervlakte van ABC is gelijk aan de som van de oppervlakten van de driehoeken PAB, PAC en PBC. Hieruit volgt het gestelde.

Deze stelling is vernoemd naar de Italiaanse wiskundige en wetenschapper Vincenzo Viviani( 1622-1703).

We kunnen de eigenschap ook veralgemenen tot een regelmatige n-hoek. In dat geval is de som van de afstanden vanuit een punt binnen de veelhoek naar de n zijden gelijk aan n keer het apothema van de veelhoek.Zelfs het omgekeerde is waar: wanneer de som van de minimale afstanden naar elk van de zijden van een veelhoek onafhankelijk is van het gekozen punt binnen de veelhoek, dan is het een regelmatige veelhoek .

De cirkel van Apollonius

Geplaatst op door

Een cirkel van Apollonius is de meetkundige plaats in het vlak van alle punten p, die bij gegeven punten A en B, voldoen aan

    \[d(P,A)=r . d(P,B)\]

De naam van deze cirkel komt van de Griekse astronoom en wiskundige Apollonius van Perga( 262-190 BC). Hij was degene die kegelsnedes, zoals ellipsen, parabolen en hyperbolen, de namen gaf die we tot op de dag van vandaag nog gebruiken. Zijn achtdelige ”Konika” over kegelsnedes wordt gezien als één van de grootste werken uit de antieke meetkunde. Verder heeft hij enorm bijgedragen aan de astronomie. Dit blijkt uit de, naar hem vernoemde, Apolloniuskrater op de maan.

Merk eerst en vooral op dat als r = 1, dat de meetkundige plaats een rechte is, namelijk de middelloodlijn van \left[A,B\right].

Veronderstel nu dan dat r \neq 1. Als we de oorsprong in A leggen, de X-as door A en B en B(d,0) noemen, dan is de nodige en voldoende voorwaarde voor (x,y) om op de meetkundige plaats te leggen gegeven door x^2+y^2=k^2( (x-d)^2+y^2. Na wat rekenwerk is dit te herleiden tot

    \[\big(x-\dfrac{k^2d}{k^2-1}\big)^2+y^2=\dfrac{k^2d^2}{(k^2-1)^2}\]

Dit is inderdaad een cirkel met middelpunt M(\dfrac{k^2d}{k^2-1},0) en straal \dfrac{kd}{k^2-1}.

Als C en D de snijpunten zijn van de cirkel met de X-as, dan geldt voor elk punt P van de cirkel dat PC en PD de deellijnen zijn van de driehoek ABP. In een driehoek worden, vanwege deze eigenschap, de cirkels door een hoekpunt en door de snijpunten van de bissectrices door dat hoekpunt met de overstaande zijde de cirkels van Apollonius van die driehoek genoemd.

Een paar opmerkingen:

  • De Apollonius cirkel door A heeft als verhouding \frac{c}{b}.
  • Elk van deze cirkels staat loodrecht op de omgeschreven cirkel van de driehoek.
  • De middelpunten van de drie cirkels liggen op één lijn.