Categorie archieven: Meetkunde

De stelling van Casey

Geplaatst op door

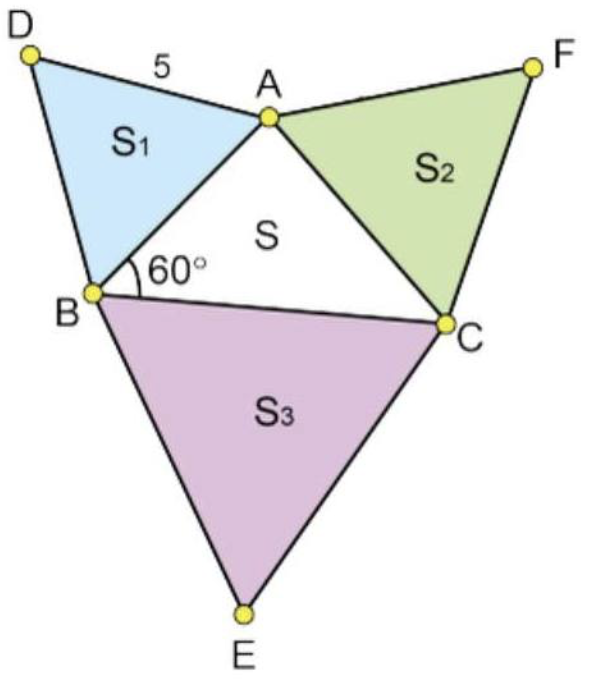
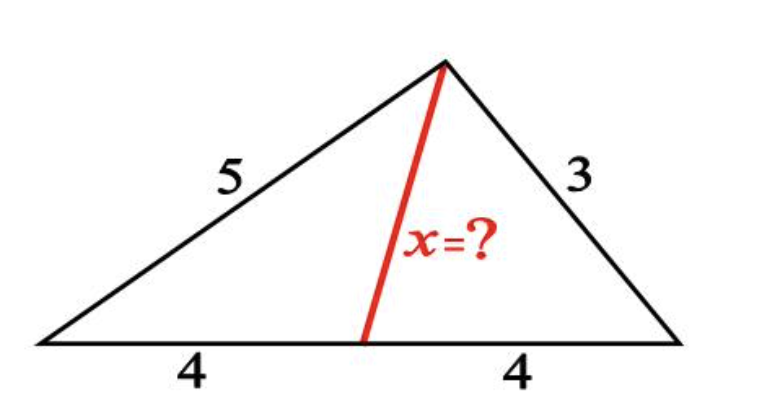
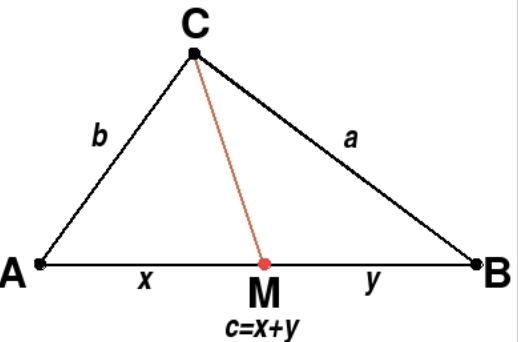
Volgende stelling komt van de hand van de Ierse wiskundige Casey   (1820-1891)

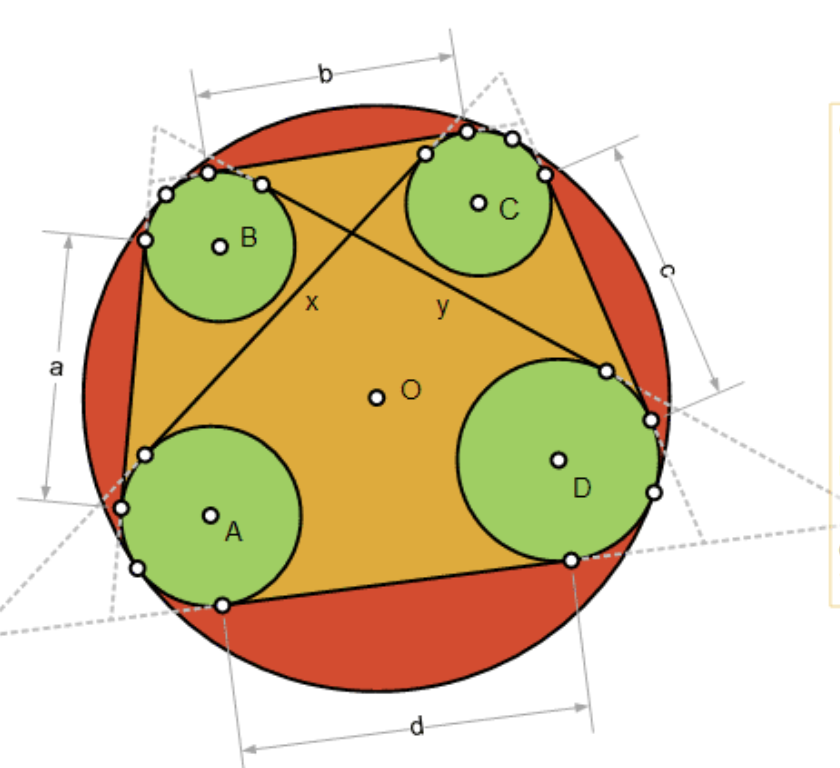
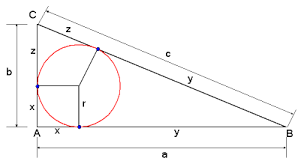
Gegeven is een cirkel, met middelpunt O en 4 niet snijdende cirkels, met middelpunten A,B,C en D) binnen die cirkel die in volgorde raken aan de grote cirkel. Noteer met aub,c,d,x en y hun gemeenschappelijke uitwendige raaklijnen. dan geldt:

    \[ac+bd=xy\]

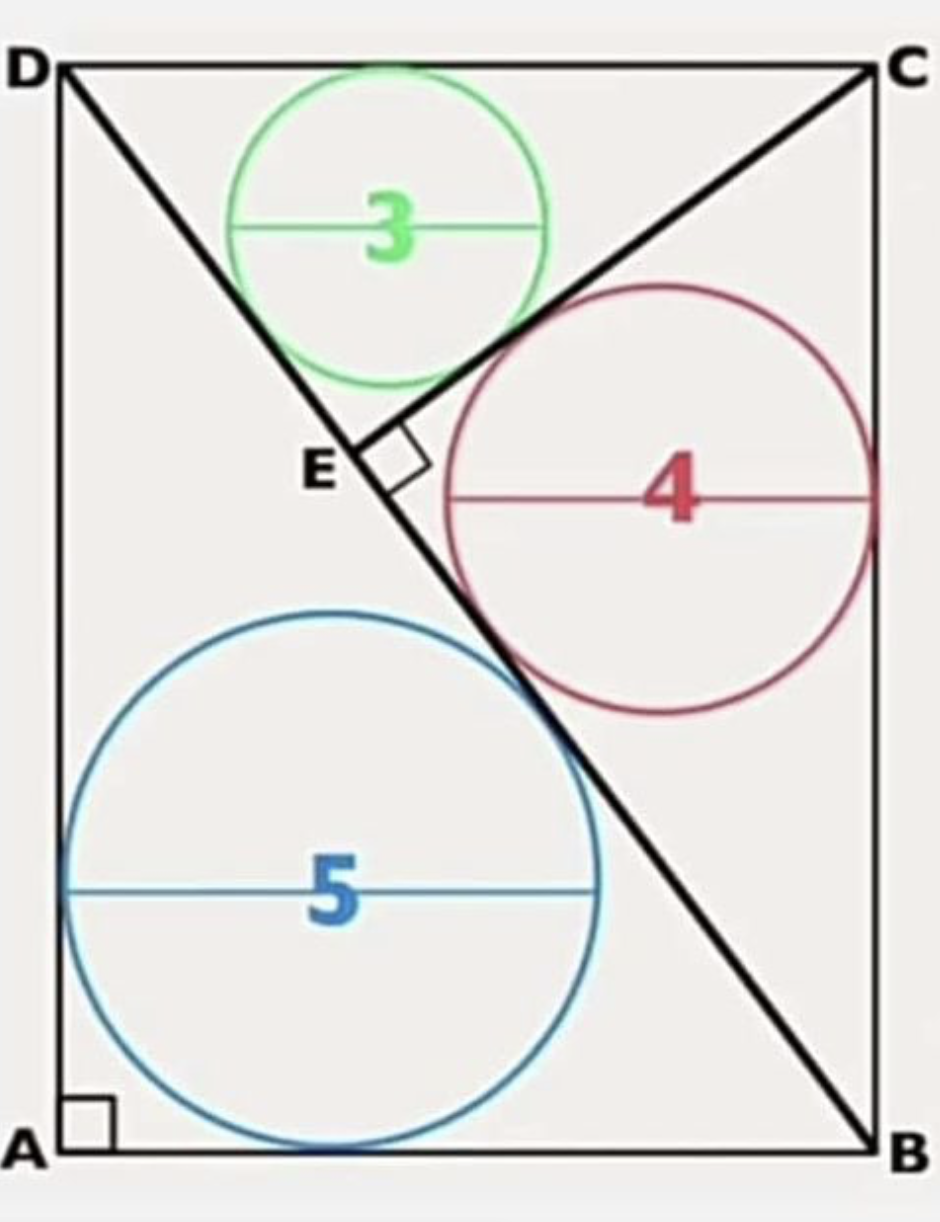
Als we de 4 binnenste cirkels laten ‘ontaarden’ in 4 punten, krijgen we de stelling van Ptolemaeus. Andere varianten bestaan er in slechts enkele cirkels te laten krimpen tot punten. Het omgekeerde resultaat is eveneens geldig.

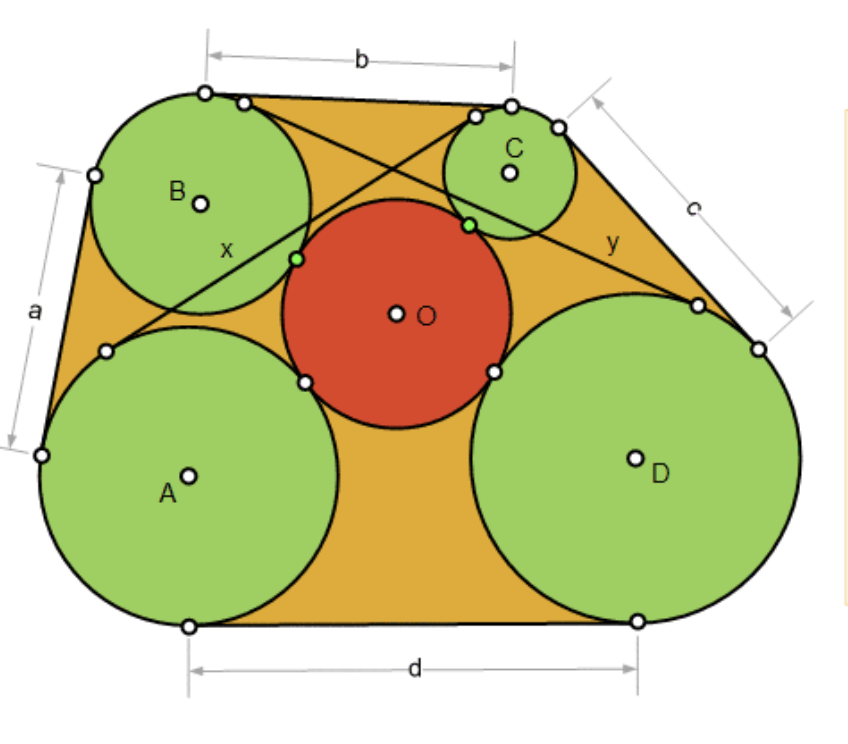
De stelling klopt trouwens ook als de 4 kleine cirkels aan de buitenkant liggen van de gegeven cirkel.

Dit artikel is het 500ste op deze website. Bedankt aan alle lezers.

Straal ingeschreven cirkel

Geplaatst op door

Zoek een verband tussen de zijden van een rechthoekige driehoek en de straal van de ingeschreven cirkel.

De stukken van de raaklijnen vanuit een punt aan de cirkel zijn even lang en bovendien is x = r.

Wanneer we a+b berekenen vinden we dat a+b=x+z+x+y=2r+c, dus geldt in een rechthoekige driehoek :

    \[a+b-c=2r\]

Kan je nu de oppervlakte van de  rechthoek ABCD berekenen?

Eutrigon stelling

Geplaatst op door

Een eutrigon is een willekeurige driehoek waarvan 1 hoek 60 graden meet. De zijde ertegenover noemt men de hypotenusa  van het eurtrigon.

Men kan op de zijden van een eutrigon gelijkzijdige driehoeken construeren, zoals in onderstaande tekening:

Er bestaat een stelling die zegt dat de som van de oppervlakten van de eutrigon en de driehoek op de hypotenusa, gelijk is aan de som van de oppervlakte van de  driehoeken op de twee andere zijden:

    \[S+S_2=S_1+S_3\]

In driehoek ABC kan je de cosinusregel toepassen:

    \[b^2=a^2+c^2-ac\]


De oppervlakte van een gelijkzijdige driehoek met zijde z wordt gegeven door de formule: \frac{\sqrt{3}z^2}{4}. Verder weten we dat de oppervlakte van driehoek ABC gegeven wordt door \frac{1}{2}ac \sin 60^{\circ}. Als we beide leden in de cosinusregel van hierboven vermenigvuldigen met \frac{\sqrt{3}}{4}, vinden we dat

    \[S+S_2=S_1+S_3\]

Stelling van Stewart

Geplaatst op door

Onlangs vond ik op Facebook volgende opgave:

Matthew Stewart (1717-1785), een Schots wiskundige, publiceerde in 1746 een stelling waarmee je dit eenvoudig kan oplossen. De stelling berekent de lengte van een hoektransversaal  d=|CM| in een driehoek:

    \[cd^2=xa^2+yb^2-cxy\]

Het bewijs ervan is eerder eenvoudig: gebruik 2 keer de cosinus regel om resp a^2 en b^2 te berekenen.

Voor die hoektransversaal kan men speciale ‘lijnen’ in de driehoek kiezen:

  • Als d de zwaartelijn is uit C, dan herleidt de formule zich tot

        \[d^2=\frac{1}{2}(a^2+b^2-\frac{1}{2}c^2)\]

    De gegeven opgave van Facebook heeft dan als oplossing x=1.
  • Als d de bissectrice is uit C, dan krijgen we

        \[d^2=ab-xy\]

    Het bewijs steunt op de bissectrice stelling x:y=b:a

 

Dit pareltje uit de vlakke meetkunde  wordt ook wel de stelling van Apollonius genoemd. Maar Apollonius van Perga formuleerde de stelling enkel voor x=y, dus het geval dat de hoektransversaal de zwaartelijn is.

 

Archimedische lichamen

Geplaatst op door

De Platonische lichamen die we zagen zijn regelmatig. Dat wil zeggen dat al hun zijvlakken identiek zijn. De Archimedische lichamen, vernoemd naar Archimedes, zijn half regelmatig, omdat ze twee of meer soorten vlakken hebben.

Alhoewel de Archimedische lichamen verschillende vlakken hebben, zijn hun hoekpunten regelmatig: ze zijn allemaal hetzelfde. Deze vormen zien er vreemder uit en zijn minder bekend, maar als we kijken naar het aantal vlakken, ribben en hoekpunten, zien we de formule terug die we ook bij de Platonische lichamen zagen : V + H – R = 2

Zeven van de Archimedische lichamen zijn gevormd door het afknotten van de platonische lichamen., met andere woorden door de hoeken er af te snijden : 

  • Afgeknotte tetraëder
  • Afgeknotte kubus
  • Afgeknotte octaëder
  • Afgeknotte dodecaëder
  • Afgeknotte icosaëder
  • Afgeknotte kuboctaëder
  • Afgeknotte icosidodecaëder

Drie andere van de Archimedische lichamen zijn gevormd door het uitbreiden van de platonische lichamen. 

  • Icosidodecaëder
  • Romboëdrische icosidodecaëder
  • Kuboctaëder

De twee laatste  Archimedische lichamen zijn gevormd door de vlakken van een kubus en een dodecaëder naar buiten te bewegen, zodat elk vlak een draai krijgt. Bij de stompe Archimedische lichamen wordt elke veelhoek omringd door gelijkzijdige driehoeken.

  • Stompe kubus
  • Stompe dodecaëder