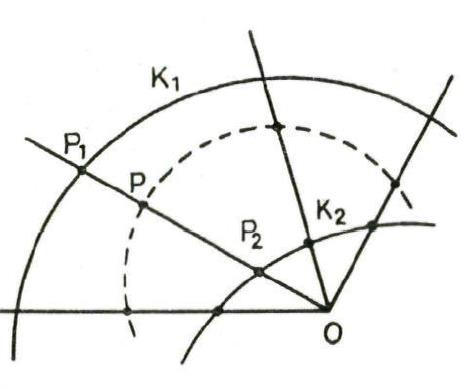
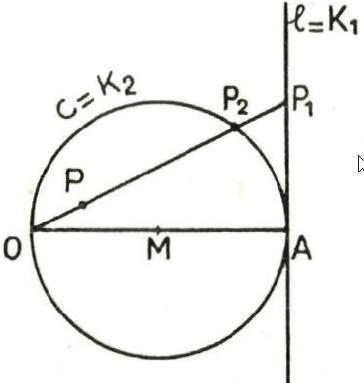
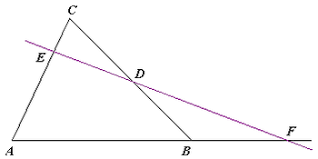
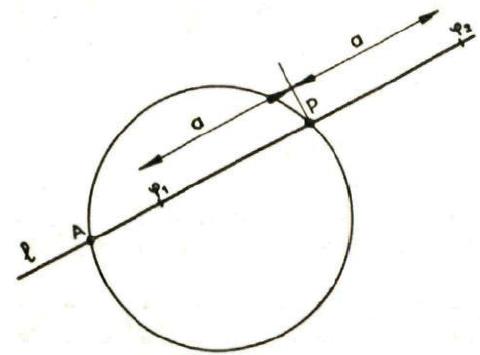
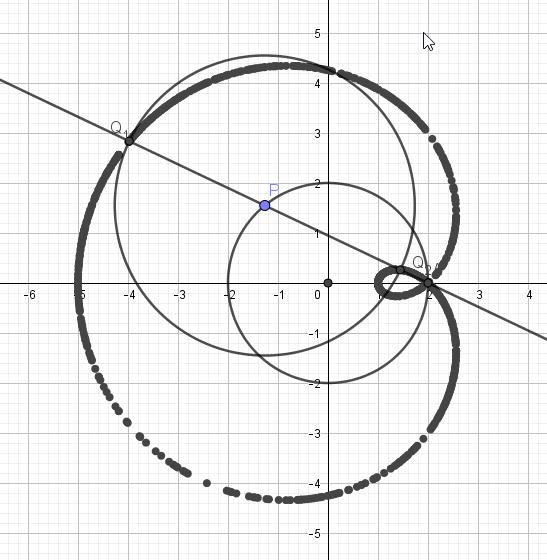
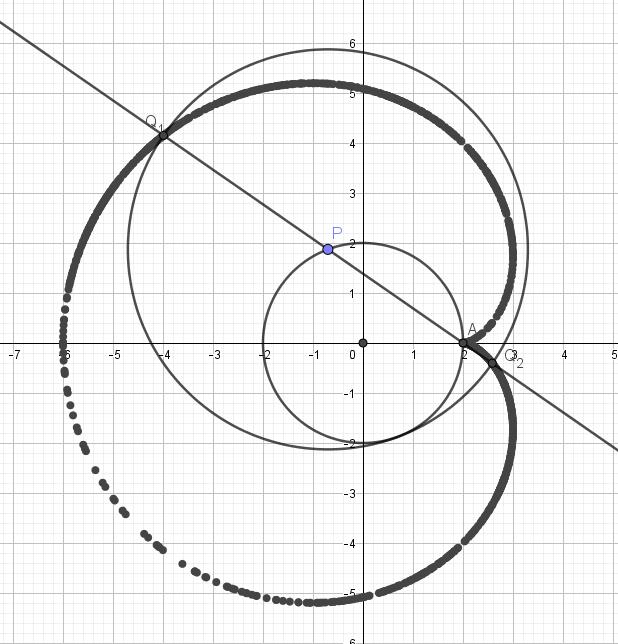
We kennen de spiegeling rond een rechte als transformatie van het vlak. De dekpunten zijn de punten van de” rechte en lengte en hoeken zijn invarianten. Maar er betaat ook een spiegeling in een cirkel: de inversie. Lees in bijgevoegde tekst hoe dit tewerk gaat en hoe je die techniek kan gebruiken om bepaalde meetkundige problemen over o.a. orthogonale cirkels en rakende cirkels, eenvoudiger op te lossen.
Het begrip inversie hebben we te danken aan de Zwitserse wsikundieg Jacob Steiner ( 1796-1863). Het wiskundige werk van Steiner beperkte zich tot meetkunde. Hij behandelde dit synthetisch en geheel niet analytisch.