Categorie archieven: Meetkunde

Arbelos

Geplaatst op door

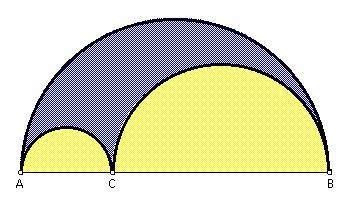
De arbelos is een meetkundige guur die bestaat uit drie aan elkaar rakende halve cirkels. De raakpunten liggen op een lijn. In onderstaande tekening is de arbelos de paarse figuur.

De arbelos is geïntroduceerd door Archimedes in zijn Liber assumptorum. Het woord arbelos komt uit het Grieks, en betekent schoenmakersmes.

In  volgende tekst kan je enkele leuke eigenschappen van de arbelos bestuderen. Dit is vrij eenvoudige meetkunde met eigenschappen van de cirkel.

Constructies in verband met verdeling

Geplaatst op door

Het gaat hier over constructies waarbij een bepaald element in een bepaalde verhoudinhg moet verdeeld worden.

Voorbeeld: Verdeel een gegeven driehoek ABC , door een evenwijdige MN aan BC , zodat de oppervlakte van driehoek AMN gelijk is aan \dfrac{9}{16} van de oppervlakte van driehoek ABC.

 

Noteer de oppervlakte van driehoek ABC door S(ABC). Dan moet
S(AMN) = \dfrac{9}{16} S(ABC) = \dfrac{9}{16}.\dfrac{1}{2}a.h. En dit betekent dat men een verdeling moet vinden zodanig dat \dfrac{9}{16}a.h=\dfrac{a}{x}.\dfrac{h}{x}. Hieruit volgt dat x=\dfrac{4}{3}, zodat de te construeren a’ en h’ gelijk moeten zijn aan a'=\dfrac{3}{4}a en h'=\dfrac{3}{4}h.

Verdeel AB in 4 gelijke delen en trek door M een evenwijdige met BC. Via de stelling van Thales weten we dat |MN|=\dfrac{3}4}|BC| en ook de hoogtes van de twee driehoeken AMN en ABC verhouden zich volgens de breuk \dfrac{3}{4}

 

Constructies in verband met verhoudingen

Geplaatst op door

In tegenstelling tot de constructies in verband met ontoegankelijkheid, waarbij spiegelingen gebruikt worden, zijn het nu de homothetieën die een hoofdrol spelen. Hierbij worden de afstanden niet bewaard, maar wel de onderlinge verhoudingen. Hierdoor wordt het mogelijk bepaalde gegevens in een zelfgekozen situatie te simuleren  om ze dan door een homothetie over te brengen naar de gekozen situatie. Hiervoor maken we gebruik van de stelling van Thales

De belangrijke keuze die men dient te maken is het kiezen van het centrum en een koppel punten.

Voorbeeld: Construeer in een driehoek ABC een lijnstuk [MN] met M op AB , N op AC en MN evenwijdig met BC zodat |NC|=3|MN|

  • Verleng AB en AC en teken DE evenwijdig met BC.
  • Construeer F op AC zodat |FD|=3|DE|.
  • Neem de homothetie met centrum A en met koppel (C,F).
  • Bepaal het beeld van DE onder deze homothetie: Dit geeft het gevraagde lijnstuk MN.

Constructies in verband met ontoegankelijkheid

Geplaatst op door

We bestuderen constructies  die we normaal gesproken wel kunnen uitvoeren, maar die nu niet uit te voeren zijn omdat bepaalde delen van de figuur ontoegankelijk zijn. Om zulke constructies uit te voeren zijn spiegelingen rond een as uitermate geschikt. We weten immers dat een spiegeling evenwijdigheid, loodrechtheid en ook afstanden en hoeken bewaart. Hierdoor wordt het mogelijk bepaalde gegevens toch bereikbaar te maken.



Bepaal de bissectrice van de twee gegeven rechten.}




    

  •  Teken een willekeurige rechte m die de twee gegeven rechten (die we a en b noemen) snijdt.
    • 

  • Spiegel de gegeven rechten rond m: a' en b'.
    • 

  • Bepaal het snijpunt S van a' en b'.
    • 

  • Construeer de bissectrice d van a' en b'. Dit is een basisconstructie.
    • 

  • Bepaal tenslotte het spiegelbeeld d', bij spiegeling van d rond m.
    • 




					

		
		
	


				
					
	

		

						
Hoektransversalen in een driehoek

			
						

				Geplaatst op   door  			

			
					


				

			
Neem een driehoek ABC. Een rechte l door een hoekpunt A van de driehoek heet hoektransversaal  of ceviaan van A. We onderzoeken onder welke voorwaarden de hoektransversalen van A,B en C door één punt gaan.


    

  1. Voor een willekeurig punt P op een hoektransversaal beschouwen we de verhouding van de afstanden tot de twee zijden.
    
Omdat \dfrac{P_1R_1|}{|P_1Q_1|}=\dfrac{P_2R_2|}{|P_2Q_2|}, is deze verhouding constant. Noem deze constante v_1 Bij elke transversaal hoort een dergelijke constante. Bereken ze met de klok mee. Nu geldt: De 3 hoektransversalen zijn concurrent als en slechts als v_1v_2v_3=1. Zo geldt bijvoorbeeld voor de binnenbissectrices van een driehoek dat v_1=v_2=v_3=1, dus: de drie binnenbissectrices van een driehoek gaan door één punt.
    2. 

  2. Laat men ook transversalen toe buiten de driehoek, dan moet men aan de constanten v_i enkel een ander teken geven. Hetr esultaat van hierboven blijft behouden.
    3. 

  3. We kunnen een hoektransversaal ook kenmerken door de verhouding u_i van de oppervlaktedelen waarin de driehoek door de ceviaan verdeeld wordt.
    
U_1=\dfrac{\text{opp} AA'C}{\text{opp} AA'B}=\dfrac{|A'C|}{|A'B|}. Het is eenvoudig te zien dat u_1u_2u_3=v_1v_2v_3 en dus geldt: De 3 hoektransversalen zijn concurrent als en slechts als u_1u_2u_3=1. Onder deze vorm is de stelling ook gekend als de stelling van Ceva.
    4. 

  4. Nu geldt bijvoorbeeld voor de zwaartelijnen van een driehoek dat u_1=u_2=u_3=1, dus: de drie zwaartelijnen van een driehoek gaan door één punt.
    5. 

  5. We kunnen dit ook ondzerzoeken voor de drie hooigtelijnen.
    
u_1=\dfrac{b \cos \gamma}{c \cos \beta}, u_2=\dfrac{c \cos \alpha}{a \cos \gamma} en u_3=\dfrac{a \cos \beta}{b \cos \alpha} en dus is u_1u_2u_3=1. Bijgevolg geldt: de drie hoogtelijnen van een driehoek gaan door één punt.
    6.