Categorie archieven: Kleine nootjes

Nootje 39

Geplaatst op 20 juni 2023 door admin

Antwoord

• 
• AH is de loodlijn uit A op BC. In een gelijkbenige driehoek verdeelt die de zijde BC in twee gelijke delen: dus elk van lengte .
• We passen nu Pythagoras toe in driehoek ABH: .
• Hetzelfde in driehoek AHM: . Hieruit volgt dat .
• Invullen in vorige formule geeft of .

 

Nootje 38

Geplaatst op 13 juni 2023 door admin

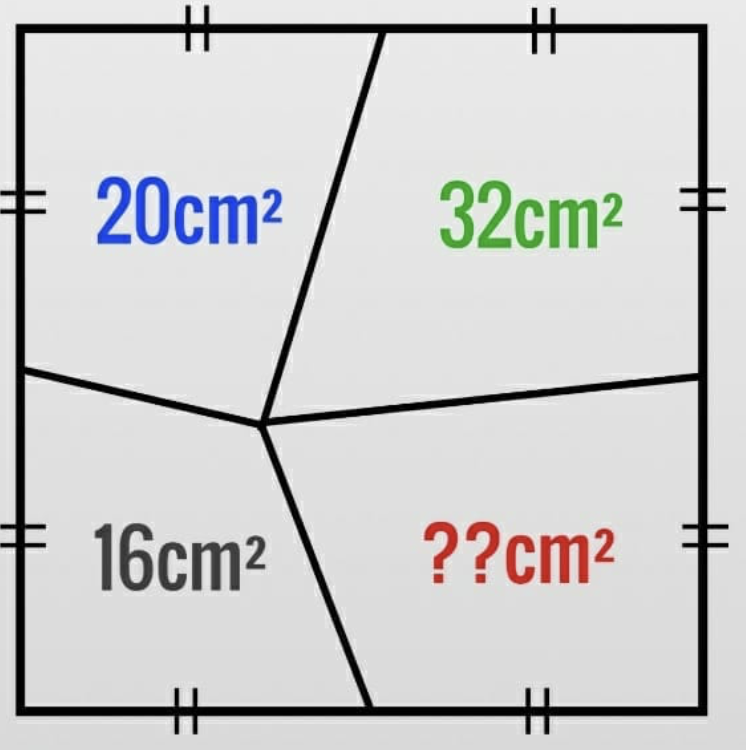
Antwoord

• Onderverdelen in driehoeken lijkt een goed idee:
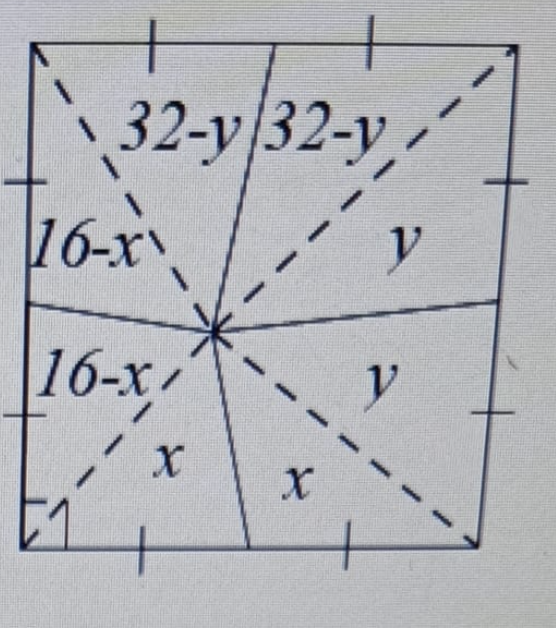
• De gelijkheid van oppervlaktes is evident: zelfde hoogte en even grote basis. 
• De vierhoek linksboven heeft oppervlakte 20 en is dus gelijk aan .
• Hieruit volgt .
• De oppervlakte van de vierhoek rechts onder, die gevraagd wordt, is gelijk aan , dus de gevraagde oppervlakte is gelijk aan 28 vierkante centimeter.

 

Nootje 37

Geplaatst op 11 juni 2023 door admin

Antwoord

• Vermoedelijk een toepassing op de stelling van Pythagoras….
• Men kan gemakkelijk bewijzen dat

     

  Dit resultaat wordt weleens de stelling van de Britse vlag genoemd, naar de vergelijking met de Union Jack
• Voor ons probleem is dus , dus is .

 

Nootje 36

Geplaatst op 27 mei 2023 door admin

Vind alle niet complexe oplossingen van

   

Antwoord

• Alles uitrekenen geeft een vierdegraadsvergelijking, die waarschijnlijk niet op te lossen is.
• We gaan de factoren in het linkerlid twee per twee uitrekenen: de eerst met de laatste en de twee middelsten.
• De opgave wordt dan:  .
• We merken op dat de twee eerste termen van de tweede factor het viervoud zijn van de eerste twee termen van de eerste factor. Stel
• We krijgen dan of na uitwerken .
• Deze vierkantsvergelijking heeft als oplossingen 1 en .
• Vervangen we y terug dan verkrijgen we twee vergelijkingen van de tweede graad. De eerste geeft als oplossingen .
• De tweede vergelijking wordt en deze heeft geen reële oplossingen.
• De enige niet complexe oplossingen zijn dus

     

Nootje 35

Geplaatst op 19 mei 2023 door admin

Zoek een getal van 6 cijfers dat begint en eindigt met een 2 en het product is van 3 opeenvolgende even getallen.

Antwoord

• Even getallen eindigen steeds op 0,2,4,6 of 8.
• Het product van drie opeenvolgende even getallen eindigt dan op , , of .
• Enkel de combinatie eindigt dus op een 2.
• Nu is en .
• Bijgevolg zijn de getallen: 64,66 en 68 en hun product is 287232.