Zijn er meer scherpe dan stompe driehoeken? Tellen dan maar. Maar dan zouden er evenveel zijn, namelijk oneindig veel. Misschien moeten we de vraag anders stellen: Neem de verzameling van alle driehoeken. Wat is de kans, dat een willekeurig genomen element van die verzameling, stomp is?
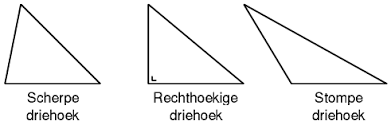
De vraag is dan uiteraard hoe we de verzameling van alle driehoeken vastleggen. Omdat de grootte van de hoeken van essentieel belang is, lijkt het gunstig om met elke driehoek een koppel getallen (x,y) te laten overeenkomen. Hierbij zijn de hoeken van de driehoek dan x,y en  . Om een driehoek te vormen moeten x en y voldoen aan:
. Om een driehoek te vormen moeten x en y voldoen aan:

De verzameling driehoeken komt dan overeen met de driehoek ABC.
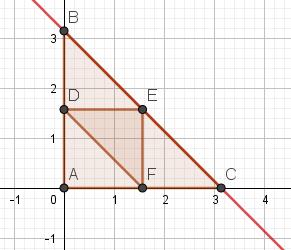
Om scherp te zijn moet x en y voldoen aan:
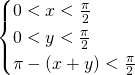
Dit komt overeen met driehoek DEF. De kans opdat een driehoek scherp zou zijn kunnen we dan berekenen door de oppervlaktes te vergelijken en dus is de kans dat een driehoek scherp is gelijk aan  . Of met andere woorden de kans dat een driehoek stomp is, is
. Of met andere woorden de kans dat een driehoek stomp is, is 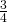 .
.
Opmerkingen:
- De punten op DE en EF geven een rechthoekige driehoek. Het is duidelijk dat de kans dat een driehoek rechthoekig is, gelijk is aan 0.
- Er zijn ook andere mogelijkheden om de verzameling driehoeken vast te leggen. Je kan bijvoorbeeld drie punten op een cirkel nemen, waarvan je één vast houdt. Je kan dan werken met omtrekshoeken en middelpunts hoeken.

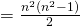 .
. dergelijke vakjes, dus
dergelijke vakjes, dus  gunstige mogelijkheden.
gunstige mogelijkheden.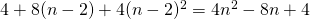 gunstige mogelijkheden. Maar die zijn dubbel geteld!
gunstige mogelijkheden. Maar die zijn dubbel geteld!![Rendered by QuickLaTeX.com \[\frac{4(n^2-2n+1)}{n^4-n^2}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-fc167443add9da972c2a8055c102e7cf_l3.png?media=1678572382)