Gebruik een goede notatie

Geplaatst op 23 oktober 2017 door admin

Het ontbreken van een goede notatie kan de verdere ontwikkeling van een wiskundig begrip tegenhouden. Net zo goed kan een goede notatie bij het oplossen van een probleem, dit probleem toegankelijker maken en ons naar een goede oplossingsmethode leiden. Het probleem wordt als het ware gecodeerd zodat het veel toegankelijker wordt.

Een voorbeeld:

Ik heb 4 kleinkinderen Mirthe (M), Tiebe (T), Joeke (J) en Nienke (N). Op hoeveel manieren kan ik 10 stukken van 2 \euro \ onder hen verdelen?

We kunnen beginnen met een paar voorbeelden:

$\begin{array}{c|c|c|c} M&T&J&N\\ \hline xx&xx&xxx&xxx\\ xxxxx&xxxxx&& \end{array}$

Bij de eerste lijn ( 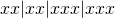$xx|xx|xxx|xxx$ ) krijgen Mirthe en Tiebe elk 2 Euro , terwijl Joeke en Nienke elk 3 Euro krijgen. Op de tweede lijn ( $xxxxx|xxxxx||$ ) krijgen Mirthe en Tiebe elk 5 Euro en Joeke en Nienke niets.
Dus met elke verdeling van de tien munten komt een rijtje van 10 x-en en 3 $|$ en overeen. Dit lijkt een goede notatie voor een verdeling .
Omgekeerd komt met elke rij van 10 x-en en 3 $|$ en een verdeling van de 10 stukken van 2 Euro overeen. Met $xxx|xxx|x|xxx$ geef ik Mirthe, Tiebe en Nienke elk 3 stukken van 2 Euro en Joeke 1 stuk.
Er zijn dus evenveel verdelingen van die 10 muntstukken over mijn kleinkinderen als er dergelijke rijtjes kunnen gevormd worden.
Het aantal van dergelijke rijtjes is een herhalingspermutatie van 13 elementen waarvan er 10 van het soort x zijn en 3 van het soort $|$ . Dus zijn er $\dfrac{13!}{10!.3!}=260$ mogelijke verdelingen.

Formuleer een eenvoudiger probleem

Geplaatst op 8 oktober 2017 door admin

Om een probleem op te lossen verzamelen we eerst alle gegevens. We proberen ze te begrijpen en te analyseren. Maar soms kunnen we dat niet doen op een betekenisvolle manier omdat de berekeningen te ingewikkeld zijn of omdat er bijvoorbeeld geen speciale gevallen zijn die ons enig inzicht kunnen geven in het probleem. We proberen dan het probleem te herformuleren in een equivalente maar eenvoudiger vorm. Hiervoor zullen we gebruik moeten maken van onze verbeelding en creativiteit. Dikwijls gebruiken we hiervoor algebraïsche of goniometrische formules, substitutie of verandering van onbekende,…

Voorbeeld:

Vind een algemene formule voor de n-de afgeleide van

$f(x)=\dfrac{1}{1-x^2}$

$f'(x)=\dfrac{2x}{(1-x^2)^2}$ , $f''(x)=\dfrac{2+6x^2}{(1-x^2)^3}$ , $f'''(x)=\dfrac{24x+24x^3}{(1-x^2)^4}$ . De uitdrukking wordt steeds ingewikkelder en we zien geen regelmaat verschijnen.
Misschien kunnen we de opgave eerst vereenvoudigen en dan denken we onmiddellijk aan splitsen in partieelbreuken:
$f(x)=\dfrac{1}{2}\Big(\dfrac{1}{1-x}+\dfrac{1}{1+x}\Big)$
Het probleem is nu herleid tot het vinden van een algemene formule voor de n-de afgeleide van $g(x)=\dfrac{1}{1-x}$ en $h(x)=\dfrac{1}{1+x}$ .
$g'(x)=\dfrac{1}{(1-x)^2}$ , $g''(x)=\dfrac{2}{(1-x)^3}$ , $g'''(x)=\dfrac{2.3}{(1-x)^4}$ . Zo komen we tot de formule:
$g^{n}(x)=\dfrac{n!}{(1-x)^{n+1}}$

We kunnen dit eventueel bewijzen via inductie.
Analoog vinden we :
$h^n(x)=\dfrac{(-1)^n.n!}{(1+x)^{n+1}}$
We besluiten dus:
$f^n(x)=\dfrac{n!}{2}\Big(\dfrac{1}{(1-x)^{n+1}}+\dfrac{(-1)^n}{(1+x)^{n+1}}\Big)$

Gebruikmaken van de symmetrie

Geplaatst op 10 september 2017 door admin

Soms kan je, door gebruik te maken van de symmetrie in de tekening of de symmetrie van de gegevens, de opgave aanzienlijk vereenvoudigen.

Een voorbeeld: Los op in $\mathbb{R}$ :

$(x+2013)(x+2014)(x+2020)(x+2021)=44$

Dit is een vierdegraads vergelijking. Hiervoor kennen we geen algemene oplossingsmethode.
Dus: haakjes uitwerken en dan ofwel proberen te ontbinden in factoren ofwel de regel van Horner toepassen. Maar dit is niet aantrekkelijk want de getallen in de opgave zijn nogal groot.
De getallen 2013,2014,2020 en 2021 liggen wel symmetrisch rond 2017!
We vervangen $x+2017$ door een nieuwe variabele $t$ . De opgave wordt nu:
$(t-4)(t-3)(t+3)(t+4)=44$

.
Dit kan je netjes uitrekenen tot:
$(t^2-16)(t^2-9)=44$
Verder uitrekenen geeft: $t^4-25t+100=0$ . Hieruit volgt dat $t^2=20$ of $t^2=5$ .
De 4 oplossingen voor $t$ zijn dan: $\pm \sqrt{5}$ en $\pm \sqrt{20}$ . En dus moet \newline $x=-2017 \pm \sqrt{5}$ of $x=-2017 \pm \sqrt{20}$ .

Zoek een patroon

Geplaatst op 2 mei 2017 door admin

Soms is het erg nuttig om een verband te zoeken tussen de data in de opgave. Kan je een bepaald patroon terugvinden? Dit kan je op weg helpen om de oplossing te vinden van je probleem.

Een voorbeeld: $f(x)$ is een veelterm is van graad 4 waarbij de coëfficiënt van $x^4$ gelijk is aan 1. Bovendien is $f(-1)=-1$ , $f(2)=-4$ , $f(-3)=-9$ en $f(4)=-16$ . Bereken $f(1)$

We weten dat $f(x)=x^4+ax^3+bx^2+cx+d$ . Uit de 4 gegevens kunnen we, via het oplossen van een stelsel, de 4 onbekenden $a,b,c$ en $d$ vinden. Eigenlijk is dat zelfs niet nodig, want we moeten enkel $f(1)$ berekenen. Maar gelukkig zien we een patroon opduiken: $-1,2,-3$ en $4$ zijn allemaal nulwaarden van de veelterm $g(x)=f(x)+x^2$ . Omdat $f(x)$ en dus ook $g(x)$ van de vierde graad is, moet $g(x)=(x+1)(x-2)(x+3)(x-4)$ . Bijgevolg is $f(1)=g(1)-1^2=23$ .

Heuristiek : Blikwissel

Geplaatst op 11 november 2016 door admin

Door onze wiskundige ervaring beperken we ons soms tot die oplossingsmethoden die in het verleden steeds gewerkt hebben. Daardoor zie je soms een eenvoudige uitkomst over het hoofd. Een belangrijke heuristiek is bijgevolg: het probleem op een andere manier bekijken. We noemen dit blikwissel.

We doen alsof we de oplossing hebben en werken zo terug tot we terechtkomen bij een situatie die we wel meester zijn. We proberen een omgekeerde redenering op te zetten door van achter naar voor werken. We leven ons in in de personen, dieren, zaken die in de vraag voorkomen en bekijken het probleem eens vanuit hun standpunt. We kijken naar andere dingen, die niet rechtstreeks gevraagd zijn. We vragen ons af wat de voorlaatste stap van de oplossing zou kunnen zijn.

Bekijken we volgend voorbeeld:

Je beschikt over twee emmers, één van 9 liter en een van 4 liter. Hoe kan je hiermee precies 6 liter water uit een waterput afmeten?

We vragen ons af wat de voorlaatste stap van de oplossing zou kunnen zijn. Om 6 liter in de emmer van 9 liter over te houden, willen we die helemaal vullen en er 3 liter uit wegnemen. Dit lukt als we in de kleine emmer 1 liter water hebben staan. Hoe kunnen we nu 1 liter maken met deze twee emmers? Nu is $1=9-4-4$ . Onze strategie is dus:

Vul de grote emmer.
Vul hiermee de kleine emmer en ledig die. Je hebt dus 4 liter uit de grote emmer weggegoten.
Giet nogmaals 4 liter van de grote emmer in de kleine en ledig die weer.
Giet de overblijvende liter in de kleine emmer.
Vul de grote emmer met 9 liter.
Giet van de grote emmer zoveel water over tot de kleine emmer helemaal gevuld is.
Nu blijft er 6 liter over in de grote emmer.

Wiskunde is leuk

Categorie archieven: Heuristieken