Veronderstel dat ![]() eindige deelverzamelingen zijn van U en noteer met
eindige deelverzamelingen zijn van U en noteer met ![]() het aantal elementen van
het aantal elementen van ![]() , dan geldt:
, dan geldt:
We noemen dit de inclusie-exclusie stelling.
Noteer ![]() de som van het aantal elementen in alle mogelijke doorsneden van i verzamelingen
de som van het aantal elementen in alle mogelijke doorsneden van i verzamelingen ![]() . Merk op dat
. Merk op dat ![]() precies
precies ![]() termen bevat. Noteer met
termen bevat. Noteer met ![]() het aantal elementen van U. Formuleren we nu een algemenere versie van vorig resultaat:
het aantal elementen van U. Formuleren we nu een algemenere versie van vorig resultaat:
Het aantal elementen van U dat tot precies m verzamelingen ![]() behoort, wordt gegeven door de formule:
behoort, wordt gegeven door de formule:
![]()
- Voor
 vinden we het aantal elementen dat tot alle
vinden we het aantal elementen dat tot alle 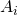 behoren.
behoren. - Voor
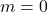 vinden we het aantal elementen dat tot geen enkele
vinden we het aantal elementen dat tot geen enkele 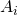 behoort.
behoort.
Vind het aantal getallen tussen 1 en 1000 dat niet deelbaar is door 2,3,5 of 7. - Stem
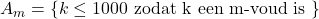 .
. - Het is eenvoudig na te rekenen dat
 ,
, 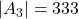 ,
, 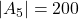 en
en  . Bijgevolg is
. Bijgevolg is 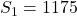 .
. - Er zijn 166 getallen die een 2 en 3 voud zijn. Er zijn 100 getallen die een veelvoud zijn van 2 en 5. Er zijn 71 getallen die een veelvoud zijn van 2 en 7. Er zijn 66 getallen die een veelvoud zijn van 3 en 5. Er zijn 47 getallen die een veelvoud zijn van 3 en 7. Er zijn 28 getallen die een veelvoud zijn van 5 en 7. Dus is
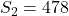 .
. - Eenvoudig narekenen geeft dat
 .
. - Er zijn 4 getallen die zowel deelbaar zijn door 2,3,5 en 7. Dus
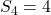 .
. - Het aantal getallen dat door geen van de cijfers 2,3,5 of 7 deelbaar is, is dan ook gelijk aan:
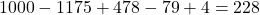 .
. - Het aantal getallen dat door één van de cijfers deelbaar is, wordt gegeven door :
 . Voor twee vinden we 265; voor drie 63 en tenslotte voor vier 4.
. Voor twee vinden we 265; voor drie 63 en tenslotte voor vier 4.
AI assistent 4.0 geeft een antwoord, maar dat is duidelijk fout!
Er zijn 720 getallen tussen 1 en 1000 die niet deelbaar zijn door 2, 3, 5 of 7. Je kunt dit aantal berekenen door alle cijfers tussen 1 en 1000 te tellen die deelbaar zijn door 2, 3, 5 of 7:
2: 500
3: 333
5: 200
7: 142
Totaal: 1225 getallen
Aantal getallen tussen 1 en 1000 die niet deelbaar zijn door 2, 3, 5 of 7: 1000 – 1225 = 720

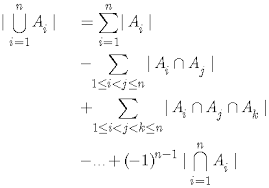

![Rendered by QuickLaTeX.com \[\sum_{n=1}^{2020}\tan n\tan(n+1)\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-e173547edeef4fe31ed6406099e30c23_l3.png?media=1678572382)

![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l}a+b+c=-1 \\ 4a+2b+c=-1\\9a+3b+c=1 \end{array} \right\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-fd99e47a9898a54e4e52f1234a93d88f_l3.png?media=1678572382)