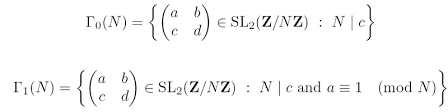De classificatie stelling van eindige enkelvoudige groepen classificeert alle eindige enkelvoudige groepen. Deze groepen zijn de bouwstenen van alle eindige groepen, zoals de priemgetallen de bouwstenen zijn van de natuurlijke getallen. De stelling beslaat meer dan 10000 pagina’s verspreid over meer dan 500 artikels in de periode van 1955 tot 1983. Michael Aschbacher en Steve Smith hebben de laatste puntjes op de spreekwoordelijke i geplaatst.
De enkelvoudige groepen zijn:
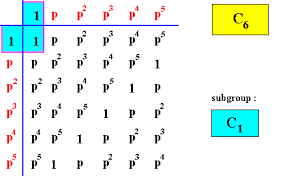
- de cyclische groepen
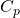 van priem orde.
van priem orde. - de alternerende groepen
 met
met 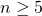 .
. - de Chevalley groepen en de gedraaide Chevalley groepen.
- De Tits groep.
- 26 sporadische groepen waaronder de 5 Mathieu groepen.
Een bespreking van al die groepen vind je in de “atlas van de eindige groepen ” van Conway,Curtis,Norton,Parker en Wilson.