De eindige rekenkunde, ook wel modulaire rekenkunde genoemd, wordt beschreven in het boek Disquisitiones Arithmeticae van Gauss, een buitengewoon invloedrijk werk uit 1801, toen de auteur nog maar vierentwintig jaar oud was.

Stel  . Indien
. Indien  en
en  bij deling door
bij deling door 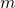 dezelfde rest geven, d.w.z. indien
dezelfde rest geven, d.w.z. indien 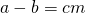 voor zekere
voor zekere  , heten
, heten  en
en  congruent modulo
congruent modulo 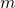 . We noteren
. We noteren  mod m.Zo is bijvoorbeeld
mod m.Zo is bijvoorbeeld 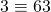 mod 5,
mod 5, 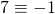 mod 8 en
mod 8 en 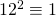 mod 13.
mod 13.
Enkele eigenschappen :
- Als
 mod m en
mod m en  mod m, dan is
mod m, dan is  mod m.
mod m.
- Als
 mod m en
mod m en 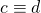 mod m, dan is
mod m, dan is  mod m.
mod m.
- Als
 mod m en
mod m en  , dan is
, dan is  mod m.
mod m.
- Als
 mod m dan is voor elke
mod m dan is voor elke  :
:  mod m.
mod m.
- Als
 mod m en
mod m en 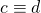 mod m, dan is
mod m, dan is  mod m.
mod m.
Rekenen met congruenties lijkt erg op het rekenen met vergelijkingen. Er is echter een belangrijk verschil: uit  mod m met
mod m met 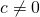 mod m hoeft niet te volgen dat
mod m hoeft niet te volgen dat  mod m. Zo is
mod m. Zo is 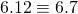 mod 10 maar 12 is niet congruent met 7 modulo 10. In andere gevallen gaat het wel op. De voorwaarde waarop de vereenvoudiging met
mod 10 maar 12 is niet congruent met 7 modulo 10. In andere gevallen gaat het wel op. De voorwaarde waarop de vereenvoudiging met  wel kan, is dat
wel kan, is dat  onderling ondeelbaar is met
onderling ondeelbaar is met  .
.
Dus als  mod m en ggd(c,m) = 1, dan is
mod m en ggd(c,m) = 1, dan is  mod m.
mod m.
Als ggd(c,m) = d, dan volgt uit  mod m dat
mod m dat  mod(
mod(  ).
).
Rekent men modulo  , dan zijn er
, dan zijn er 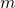 verschillende soorten getallen, al naar gelang ze verschillende resten geven bij deling door
verschillende soorten getallen, al naar gelang ze verschillende resten geven bij deling door 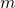 . De verzameling van alle gehele getallen die eenzelfde rest geven heet een restklasse modulo
. De verzameling van alle gehele getallen die eenzelfde rest geven heet een restklasse modulo 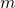 . Er zijn dus precies
. Er zijn dus precies 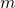 verschillende restklassen modulo
verschillende restklassen modulo 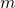 . De restklasse die een getal
. De restklasse die een getal  bevat, noteert men als
bevat, noteert men als 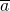 . Deze notatie is natuurlijk niet eenduidig bepaald, want als
. Deze notatie is natuurlijk niet eenduidig bepaald, want als  mod m, stellen
mod m, stellen 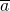 en
en 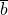 dezelfde restklasse modulo
dezelfde restklasse modulo 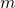 voor en omgekeerd.
voor en omgekeerd.
Werken we modulo 4 dan is 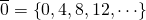 ,
,  ,
,  ,
,  .
.
Men kan in de verzameling restklassen modulo 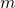 , genoteerd door
, genoteerd door 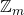 , een optelling en een vermenigvuldiging defini\”eren via
, een optelling en een vermenigvuldiging defini\”eren via  en
en 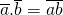 . Deze rekenregels lijken erg op de regels van optelling en vermenigvuldiging van gehele getallen.
. Deze rekenregels lijken erg op de regels van optelling en vermenigvuldiging van gehele getallen.
Eigenschappen :

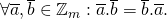
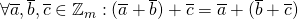 .
. .
. .
.
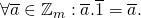
- Er is een unieke restklasse
 met
met  , namelijk
, namelijk  .
.
Veronderstel dat we de rest willen bepalen van  bij deling door 7. Omdat
bij deling door 7. Omdat 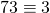 mod 7 en
mod 7 en 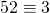 mod 7, moet
mod 7, moet 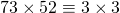 mod 7
mod 7 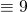 mod 7
mod 7  mod 7. Dus de rest bij deling van
mod 7. Dus de rest bij deling van  door 7 is 2. We moeten daarvoor het product niet uitrekenen.
door 7 is 2. We moeten daarvoor het product niet uitrekenen.
![]() . Een rekenkundige functie drukt een zekere eigenschap van de natuurlijke getallen uit. Een rekenkundige functie
. Een rekenkundige functie drukt een zekere eigenschap van de natuurlijke getallen uit. Een rekenkundige functie ![]() is multiplicatief als voor elk tweetal onderling ondeelbare getallen
is multiplicatief als voor elk tweetal onderling ondeelbare getallen ![]() en
en ![]() geldt dat
geldt dat ![]()