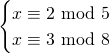Als p een priemgetal is en a en p onderling ondeelbaar zijn dan geldt:
![]()
Uit deze stelling, die de kleine stelling van Fermat genoemd wordt en in 1640 een eerste keer vermeld werd, volgt dat voor elke a en voor een priemgetal p geldt dat
![]()
De stelling wordt bijvoorbeeld gebruikt om de restklasse modulo een groot getal uit te rekenen. Bereken bijvoorbeeld de rest bij deling van ![]() door 11. Volgens de kleine stelling van Fermat is
door 11. Volgens de kleine stelling van Fermat is ![]() , dus is
, dus is ![]() .
.
Er bestaat een veralgemening voor de stelling, die zegt dat als a en m onderling ondeelbaar zijn, geldt
![]()
Hierbij is ![]() de totiënt functie van Euler die het aantal getallen, kleiner dan m, berekent die onderling ondeelbaar zijn met m. Deze stelling wordt de Euler-Fermat stelling genoemd.
de totiënt functie van Euler die het aantal getallen, kleiner dan m, berekent die onderling ondeelbaar zijn met m. Deze stelling wordt de Euler-Fermat stelling genoemd.




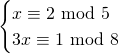 of
of