Categorie archieven: Getaltheorie

Algebraïsche getallen

Geplaatst op door

Een algebraïsch getal is een wortel van een van 0 verschillende veelterm met rationale coëfficiënten.

Zo is \sqrt{2} een reëel algebraïsch getal want \sqrt{2} is een wortel van de veelterm x^2-2. Verder is bijvoorbeeld \sqrt{2}i een complex algebraïsch getal want \sqrt{2}i is een wortel van de veelterm x^2+2.

Enkele eigenschappen:

  • het tegengestelde van een algebraïsch getal is ook een algebraïsch getal.
  • het omgekeerde van een van 0 verschillend algebraïsch getal is ook een algebraïsch getal.
  • elk rationaal getal is een algebraïsch getal.
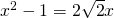  • ook de som en het product van 2 algebraïsche getallen zijn algebraïsch. Dit is niet zo evident. Neem bijvoorbeeld x=\sqrt{2}+\sqrt{3}, de som van 2 algebraïsche getallen. Dan is x-\sqrt{2}=\sqrt{3}, wat na kwadrateren x^2-1=2\sqrt{2}x geeft. Nogmaals kwadrateren geeft uiteindelijk 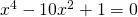x^4-10x^2+1=0.Bijgevolg is x een algebraïsch getal.
  • uit al de vorige eigenschappen kan je dus besluiten dat de algebraïsche reële getallen en de algebraïsch complexe getallen, allebei met de gewone optelling en vermenigvuldiging, velden zijn.
  • men kan zelfs bewijzen dat r een reëel algebraïsch getal is als r een wortel is van een van 0 verschillende veelterm met gehele coëfficiënten.
  • we noteren \mathbb{A} voor het veld van de reële algebraïsche getallen. Dan is \mathbb{Q} \subset \mathbb{A}\subset \mathbb{R}.

Een transcendent getal is een getal dat niet algebraïsch is. Het bestaan van transcendente getallen is niet vanzelfsprekend. dat ze inderdaad bestaan is bewezen door de Franse wiskundige J.Liouville(1809-1882). 

De transcendentie van e, de basis van de natuurlijke logaritmen, werd in 1873 bewezen door C.Hermite(1829-1901). De transcendentie van \pi werd op een gelijkaardige manier bewezen in 1882 door F.Lindemann(1852-1939)

Cantor bewees dat de verzameling van de complexe algebraïsche getallen aftelbaar oneindig is, met andere woorden ze bezit dezelfde kardinaliteit als de verzameling van de natuurlijke getallen. De stelling van Cantor houdt in dat de verzameling van de transcendente complexe getallen de overaftelbaar is. Dus bijna alle complexe getallen zijn transcendent! In de beginafbeelding zie je de algebraïsche complexe getallen.

Stelling van Wilson

Geplaatst op door

De kleine stelling van Fermat zegt ons dat voor een priemgetal p geldt dat a^p \equiv a \mod{p}. Maar dan zijn 1,2, … , p – 1 allemaal nulpunten van de veelterm X^{p-1}-1 in de verzameling \mathbb{Z}_p[X] en dus kunnen we, omdat er geen nuldelers zijn, volgende ontbinding neerschrijven: X^{p-1}-1 = (X-1)(X-2) \cdots (X-(p-1)).
Door hierin X te vervangen door 0, vinden we een deel van volgende stelling:

    \[p \text{ is priem als en slechts als } (p-1)! \equiv -1 \mod{p}\]

Dit resultaat staat bekend als de stelling van Wilson, naar de Engelse wiskundige John Wilson (1741-1793). Nochtans komt dit resultaat een eerste keer voor bij Abu Ali al-Hasan ibn al-Haytham (965-1040)

Bovendien had Wilson geen bewijs van de stelling. Het was Lagrange die in 1771 het eerste bewijs ervan formuleerde.

Het is ook duidelijk dat als n een samengesteld getal is, groter dan 4,  dat  (n-1)! \equiv 0 \mod{n}.

Een algemene vorm is voor ieder oneven priemgetal p en voor ieder positief geheel getal k kleiner dan p:

    \[(k-1)!(p-k)! \equiv (-1)^k \mod{p}\]

Deze veralgemening danken we aan C.F.Gauss

Pseudopriemen

Geplaatst op door

De kleine stelling van Fermat leert ons dat voor een priemgetal p geldt dat

    \[a^{p-1} \equiv 1 \mod p\]

of voor getallen a die onderling ondeelbaar zijn met p: a^p \equiv a \mod p.

De stelling van Fermat is niet omkeerbaar. Inderdaad is  2^{340} \equiv 1 \mod 341 en 341 = 11 \times 31. In de vijfde eeuw voor onze jaartelling wisten de Chinezen al dat uit p priem volgt dat 2^{p-1} \equiv 1 \mod p. Zij waren ook overtuigd van het omgekeerde. Ook Leibniz was daarvan overtuigd. Slechts in 1819 vond F. Sarrus bovenvermeld tegenvoorbeeld.

We noemen 341 een pseudopriem t.o.v. de basis 2.

Een Carmichael getal is een getal  p dat niet priem is en waar voor alle a die onderling ondeelbaar zijn met p, toch geldt dat a^{p-1} \equiv 1 \mod p. Zo is bijvoorbeeld 561 het kleinste Carmichael getal. De volgende Carmichael getallen zijn  1105, 1729, 2465, 2821, 6601, 8911, 10585, 15841 en  29341. Pas in 1994 werd bewezen dat er oneindig veel Carmichael getallen zijn.

De naam Carmichael getal komt van de Amerikaanse wiskundige  Richard David  Carmichael ( 1979-1967) die het bestaan ervan introduceerde in 1910. Een andere naam voor deze getallen is absolute pseudopriemen

Priemgetaltest

Geplaatst op door

We willen twee fundamentele vragen uit de getaltheorie even onder de aandacht brengen:

  1. Hoe kan men snel zien of een getal een priemgetal is?
  2. Als n niet priem is, hoe vindt men gehele getallen a en b , groter dan 1, zodat n = a.b?

Het is verbazingwekkend dat men dikwijls kan weten dat een getal niet priem is, zonder er een factor van te kennen. Dat is te danken aan de stelling van Fermat: als n priem is dan geldt voor elk geheel getal a dat

    \[a^n \equiv a \mod n\]

Dus als je een geheel getal a kan vinden waarvoor a^n niet gelijk is aan a modulo n, dan weet men zeker dat n niet priem is, zonder nochtans een factor van n te kennen.

Willen we bewijzen dat een getal toch priem is, dan hebben we een omkering van de stelling  van Fermat nodig. Hier doen zich twee moeilijkheden voor:

  • De directe omkering is gewoon fout! Het getal n = 1729 = 7.13.19 is niet priem en toch is  a^{1729}\equiv a \mod 1729 voor elk geheel getal a.
  • En zelfs al zou de omkering waar zijn, dan zou ons dat niet echt helpen want het is ondoenlijk alle gehele getallen a te proberen.

Het zoeken naar oplossingen van deze problemen is zeer actueel en de gevonden methoden zijn soms zelfs futuristisch, aangezien ze steunen op het nog onbewezen vermoeden betreffende de veralgemeende Riemannhypothese.  Enkele namen die op dit gebied een belangrijke bijdrage geleverd hebben zijn: R. Solovay, V.Strassen, G.L. Miller, M.O.Rabin en  H.W. Lenstra ( zie foto)

De kleine stelling van Fermat

Geplaatst op door

Als p een priemgetal is en a en p onderling ondeelbaar zijn dan geldt:

    \[a^{p-1} \equiv 1 \text{ mod } p\]

Uit deze stelling, die de kleine stelling van Fermat genoemd wordt en in 1640 een eerste keer vermeld werd, volgt dat voor elke a en voor een priemgetal p geldt dat

    \[a^p \equiv a \text { mod } p\]

De stelling wordt bijvoorbeeld gebruikt om de restklasse modulo een groot getal uit te rekenen. Bereken bijvoorbeeld de rest bij deling van 2^{245} door 11. Volgens de kleine stelling van Fermat is 2^{10} \equiv 1 \text{ mod } 11, dus is 2^{245} \equiv (2^{10})^24.2^5 \equiv 2^5 \equiv 10 \text{ mod } 11.

Er bestaat een veralgemening voor de stelling, die zegt dat als a en m onderling ondeelbaar zijn, geldt

    \[a^{\varphi(m)} \equiv 1 \text { mod }m\]

Hierbij is \varphi(m) de totiënt functie van Euler die het aantal getallen, kleiner dan m, berekent die onderling ondeelbaar zijn met m. Deze stelling wordt de Euler-Fermat stelling genoemd.