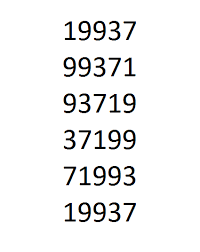Een circulair priemgetal is een priemgetal dat een priemgetal blijft bij elke cyclische rotatie van de cijfers . Zo is 13 een circulair priemgetal, want het is priem en ook 31 is een priemgetal.
Het is duidelijk dat een circulair priemgetal nooit het cijfer 0,2,4,5 of 8 kan bevatten, want door een cyclische permutatie komt dat cijfer ooit achteraan en dan is het getal deelbaar door 2 of 5 en dus niet priem.
De eerste circulaire priemen zijn 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, 97, 113, 131, 197,…
Er is een stelling die zegt dat elk priemgetal dat enkel bestaat uit enen, altijd een circulair priemgetal is. Eveneens beweert men dat er oneindig veel priemgetallen bestaan met enkel enen. Dus zijn er ook oneindig veel circulaire priemgetallen. Waarschijnlijk zijn er, vanaf 1000000, geen andere dan die met enkel enen.