Als twee gehele getallen gelijk zijn, dan zijn hun resten bij deling door een zelfde natuurlijk getal, verschillend van nul, ook gelijk. Of via contrapositie: als er tenminste 1 natuurlijk getal n bestaat waarvoor ![]() , dan zal ook a verschillend zijn van b.
, dan zal ook a verschillend zijn van b.
Proberen we eens met
![]()
- Herschrijf tot
 .
. - We bepalen de resten van beide leden bij deling door 3:
 .
. - Of
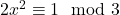 .
. - Het inverse element, modulo 3, van 2 is 2 zelf, dus kunnen we vorige vergelijking herschrijven als
![Rendered by QuickLaTeX.com \[x^2\equiv 2 \mod 3\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-d5ec2e26c2d672d8eadaca3e32f7b972_l3.png?media=1678572382)
- Nu is 2 geen kwadraatrest modulo 3, want
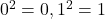 en
en 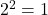 .
. - Bijgevolg heeft de gegeven vergelijking geen oplossingen.

![Rendered by QuickLaTeX.com \[\begin{array}{c|c|c} x&3x-4y&y \\ \hline \\1&-5&2\\-1&5&-2\\5&-1&4\\-5&1&-4\end{array}\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-a0e6374012fcaa9c4b8646c131b1d3a3_l3.png?media=1678572382)
![Rendered by QuickLaTeX.com \[\left\{\begin{matrix}x=-265+44w\\y=302-50w\\z=163-27w\end{matrix}\right\]](https://usercontent.one/wp/www.wiskundemagie.be/wp-content/ql-cache/quicklatex.com-d7ab45b4bcb09602fbe3738318cb5b21_l3.png?media=1678572382)