Categorie archieven: Geschiedenis

4.Egyptische wiskunde

Geplaatst op door

Onze grootste kennis van de Egyptische wiskunde komt van twee papyri: Rhind ( rond 1450 v.C.) en Moscou (1750 v.C)

De Egyptenaren gebruikten een tientallig stelsel met volgende tekens:

 

 

 

 

 

 

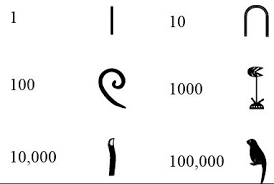
De notatie is in wezen additief:

Enkele merkwaardigheden:

  • Om te vermenigvuldigen gebruikten ze een reeks van verdubbelingen. De vermenigvuldiging wordt dus herleid tot een aantal optellingen. Eén van de getallen werd dus in feite  binair herschreven. Zo wordt 25 x 13 = (16 + 8 + 1) x 13.
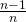  • De Egyptenaren rekenden met stambreuken en eventueel hun complement: \frac{1}{n} of  \frac{n-1}{n}. Een stambreuk werd genoteerd als 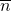\overline{n}. Alle andere breuken trachtten ze te schrijven als som van stambreuken, waarbij elke stambreuk slechts één keer mag voorkomen. ze kenden hiervoor enkele formules zoals bvb. \frac{2}{3n}=\frac{1}{2n}+\frac{1}{6n}.
  • De deling werd beschouwd als een vermenigvuldiging met een stambreuk. Zo is het quotiënt van 13 door 21 gelijk aan (1+4+8).\overline{21}=\overline{21}+2.\frac{2}{21}+4\frac{2}{21}=\overline{21}+2.(\frac{1}{42}+\frac{1}{14})+4(\frac{1}{42}+\frac{1}{14})=\overline{21}+\overline{2}+\overline{14}.
  • De rekenkunde van de Egyptenaren was minder gevorderd dan die van de Babyloniërs.
  • Met de meetkunde was het anders gesteld, deze wordt wel eens  ” een geschenk van de Nijl ” genoemd. Toch vertoonde de meetkunde nooit een deductieve structuur.
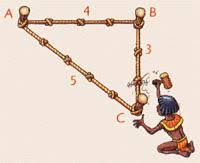
  • Als iemand bij de jaarlijkse overstromingen van de Nijl land verloor, moest hij dit aan de farao melden. Deze stuurde dan dienaren die het verlies gingen opmeten en een proportionele belastingsvermindering toestonden. Het opmeten, en eventueel herverkavelen, was het werk van de harpedonapten, die gebruik maakten van touwen waarin op regelmatige afstanden knopen lagen. Zo maakten ze bvb. gebruik van de eigenschap: een driehoek waarvan de zijden 3-4-5 lengte hebben , is rechthoekig.
  • Ze kenden een formule voor de inhoud van een afgeknotte vierkantige piramide.
  • De jaarlijkse overstromingen gaven ook aanleiding tot kalenderrekening en astronomie.
  • Voor 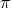\pi gebruikten ze een heel goede benadering : 3,1605.
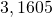  • De Egyptische wiskunde heeft zich meer dan 2000 jaar kunnen ontwikkelen, maar starre staatsstructuren en geheimhouding door priesters verhinderden een ongeremde ontwikkeling. In het eerste millenium voor Christus zou een beschaving opstaan die op wiskundig gebied de Egyptische en Babylonische ver zou overvleugelen: de Griekse.

3.Wiskunde in Mesopotamië

Geplaatst op door

 

Mesopotamië wordt beschouwd als de bakermat van onze beschaving: het schrift, het wiel en de woonentiteit, die we nu ‘stad’ noemen, waren uitvindingen van de verschillende beschavingen die achtereenvolgens het gebied beheersten: Soemerë, Ur, Akkad en Babylonië. 

Het Mesopotamisch numeriek systeem is zestigdelig en positioneel:

POSITIONEEL : De cijfers van 1 tot 59 werden voorgesteld door een combinatie van 2 symbolen: het eenheidssymbool en het tien-symbool. 

ZESTIGDELIG : 1.60³+57.60²+46.60+40 = 424000

 

Het getal 0 kenden ze niet. Optellen en aftrekken ging erg vlot. Het vermenigvuldigen had wat meer voeten in de aarde. In ons tientallig stelsel, moeten de tafels tot en met 9 bekend zijn om te kunnen vermenigvuldigen.  Doordat ze echter gebruik maakten van een zestigtallig stelsel moesten alle tafels tot en met 59 bekend zijn om verder te rekenen. Zij hadden per tafel 23 producten nodig: van 1 tot en met 20, 30, 40 en 50. In totaal dus 59 × 23 = 1357 producten. Er zijn ook kleitabletten met hierop de kwadraten van 1 tot en met 59 gevonden.  Door gebruik te maken van de formule :

    \[a.b = \frac{1}{2}\Big((a+b)^2-a^2-b^2\Big)\]

 

    \[a.b=\frac{1}{4}\Big((a+b)^2-(a-b)^2\Big)\]

konden ze via de tabellen met kwadraten ook vermenigvuldigingen uitvoeren. Om een deling uit te voeren hadden ze een tabel waarin de omgekeerden stonden van hun basisgetallen.

Lange tijd werd gedacht dat de Babyloniërs niet aan meetkunde deden, maar alleen rekenden om bijvoorbeeld voedselvoorraden bij te houden. maar men heeft kleitabletten gevonden waar twee intervallen op staan wanneer Jupiter aan de horizon verschijnt. De positie van de planeet wordt berekend op zestig en honderdtwintig dagen. De tekst bevat geometrische berekeningen gebaseerd op het oppervlak van een trapezium met lange en korte zijden.

 

We geven een paar voorbeelden uit de praktijk van de Babylonische wiskunde:

  • Een methode om de verhouding van de diagonaal tot de zijde van een vierkant te berekenen: Een vierkant met zijde 30 heeft een diagonaal 42;25,35. Daaruit wordt de verhouding van de diagonaal tot de zijde berekend als 1;24,51,10 of omgerekend in ons tiendelig stelsel 1,4142130 wat ongeveer de vierkantswortel uit 2 is.


  • Pythagorese drietallen  in het tablet Plimton 322:

2.De beschavingen van de riviervalleien

Geplaatst op door

Ongeveer 10000 jaar geleden veranderde de Neolithische revolutie voor altijd de interactie tussen de mens en de wereld om ons heen door de invoering van het basis ingrediënt dat beschaving mogelijk maakt: de landbouw.

Voorafgaand aan de Neolithische agrarische revolutie, leefden de mensen ​​als jager-verzamelaars, constant in beweging om zichzelf te voeden. Ze waren georganiseerd in kleine nomadische groepen, meestal van rond de twintig tot dertig mensen. Ze waren niet in staat om in grote populaties te leven vanwege hun beperkte voedselvoorziening en de noodzaak om te blijven bewegen.

De Neolithische agrarische revolutie vond zijn oorsprong in het Midden-Oosten, waarschijnlijk vanwege het gunstige klimaat. Maar na verloop van tijd werd de landbouw verspreid naar andere vruchtbare gebieden rond rivieren, zoals Egypte rond de Nijl en de Indus vallei.

De voornaamste reden was de beschikbaarheid van water. grote hoeveelheden water en vruchtbare grond, bevorderd door regelmatige overstromingen, zorgden voor overvloedige landbouwproductie en niet alle beschikbare arbeid moest voor de landbouw worden gebruikt. Zo was het voor sommige leden van de gemeenschap mogelijk andere activiteiten te beoefenen, zoals bouw, handel of administratie.

Het is duidelijk dat hierdoor een sterke behoefte ontstond aan het beoefenen van activiteiten zoals meten en vergelijken van hoeveelheden, die noodzakelijk werden om handel te drijven, opmeten van landerijen vereist om eigendommen te verdelen en de studie van de bewegingen van zon, maan en planeten die leidden  tot het berekenen van een kalender en het bepalen van seizoenen. Deze activiteiten werden uiteraard sterk bevorderd door wiskundig denken.

1. Vroegste sporen van wiskundig denken

Geplaatst op door

Het is onmogelijk te bepalen wanneer de primitieve mens vertrouwd geraakte met basis begrippen zoals hoeveelheden en vormen. Het staat wel vast dat ruim 30000 jaar geleden de mens reeds  verder dacht dan de hoeveelheden één, twee en meer. Hij toonde ook interesse is regelmatig weerkerende verschijnselen zoals de opeenvolging van de dagen, de maanfasen of de wisseling van de seizoenen.

De primitieve mens vertrok uit Afrika om de rest van de wereld te bevolken. Een aantal ‘bewijzen’ van hun eerste wiskundig denken:

  • Het Lebombo beentje: Het is een gekerfd beentje, gedateerd op ca. 35.000 jaar v.Chr. Het werd gevonden in het Lebombo gebergte ergens tussen  Zuid-Afrika en Swasiland.  Het vertoont overeenkomsten met de kalenderstokjes . Het geeft niet aan dat de mensen in staat waren om te rekenen, maar wel om te tellen en een bepaalde cyclus te achterhalen.
  • Het Ishango beentje: Het werd gevonden nabij Ishango ( Belgisch Congo) en is ongeveer 22000 jaar oud. Men vermoedt dat het om telstokjes gaat, waarbij basis 6 en 10 worden gebruikt.
    De eerste kolom geeft alle priemgetallen tussen 10 en 20. Totale som 60. De som van de tweede kolom is 48 en van de derde is terug 60. In d ederde kolom komen de getallen voor die 1 verschillen van een tiental: 9,11,19 en 21.
  • Rotsschilderingen  tonen de mogelijkheid van de primitieve mens om ongeveer 35000 jaar geleden figuratieve en abstracte vormen weer te geven.

Agnesi

Geplaatst op door

Maria Agnesi ( 16 mei 1718 – 9 januari 1799 ) was een Italiaanse taalkundige en wiskundige. Ze was de eerste vrouw die een boek schreef over de differentiaal en integraalrekening.

In haar jeugd blonk ze uit door haar kennis van talen ( Grieks, Hebreeuws, Spaans, Duits, Latijn en waarschijnlijk nog een paar andere talen ). Bij haar thuis werden de geleerdste mensen uit Bologna uitgenodigd , waarvoor zij allerlei filosofische problemen besprak.

Op haar twintigste stopte ze daarmee en hoewel haar wens was om non te worden, wijdde ze zich van dan af volledig aan de wiskunde. Haar belangrijkste werk was Instituzioni analitiche ad uso della gioventù italiana,

Op haar vierendertigste volgde ze uiteindelijk haar droom en studeerde theologie. Ze richtte een bejaardentehuis, Opera Pia Trivulzio, op en bestuurde het, terwijl ze leefde  zoals de nonnen die daar werkten.

We kennen haar ook van de kromme met de naam de heks van Agnesi.

De kromme heeft vergelijking y(1 + x²) = 1. Ze  ontstaat wanneer je een rechte lijn over een cirkel laat ronddraaien . De kromme heette daarom oorspronkelijk een ‘versiera’ (afgeleid van het Latijnse vertere = draaien). Het woord ‘versiera’ was echter ook een afkorting van ‘avversiera’ of ‘vrouw van de duivel’.