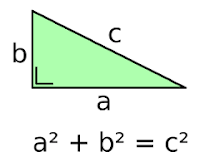De bloeitijd van de school van Pythagoras (550-450 v. C.)
Pythagoras( 580-497 v.C.) was de stichter van het filosofisch-religieus-wetenschappelijk genootschap dat in Croton( Zuid-Italie) rond het midden van de 6 de eeuw voor Christus tot ontwikkeling komt en waarvan de leden ( Pythagoreeers genoemd) zich later over de Griekse steden in Zuid-Italie verspreiden. Volgens hun leer moet de onsterfelijke ziel gereinigd worden door het onderhouden van strenge leefregels ( Acusmata) en door de studie van muziek, getallenleer, meetkunde en sterrenkunde ( de 4 Mathemata). Elke abstracte of concrete werkelijkheid kan door een natuurlijk getal voorgesteld worden. Alle ontdekkingen worden aan de meester (Pythagoras) opgedragen zodat er geen namen van wiskundigen uit die tijd bekend zijn. Na zijn dood valt de school uiteen in verschillende sektes: de Mathematicoi die een haast zuiver wetenschappelijke richting uitgaan en de Acuslaticoi die trouw blijven aan de strenge leefregels. Tot deze laatste groep hoort een Pythagoraeeer die het bestaan van een irrationaal getal ontdekt en daardoor het ganse Pythagorische wereldbeeld laat instorten. De meeste sekten worden rond 430 v.C. door de Atheense aristocratie uit Zuid-Italie verbannen.
De grootste verdienste van de Pythagoreeers bestaat hierin dat zij de wiskunde, en vooral de meetkunde, definitief bevrijd hebben van utilitaire motieven.
Behandelde onderwerpen uit de meetkunde :
- stelling van Pythagoras
- som van de hoeken van een driehoek
- hoeken die ontstaan door twee evenwijdigen te snijden met een derde rechte
- oppervlakte van een willekeurige veelhoek
- eigenschappen van hoeken en bogen in een cirkel
De Pythagorische meetkunde vertoont veel sporen van Babylonische herkomst; zo zijn er een hele reeks stellingen die duidelijk het meetkundig verlengstuk zijn van algebraische vraagstukken . We vinden bijvoorbeeld de formule ![]() als betrekkingen tussen oppervlakten van rechthoeken en vierkanten.
als betrekkingen tussen oppervlakten van rechthoeken en vierkanten.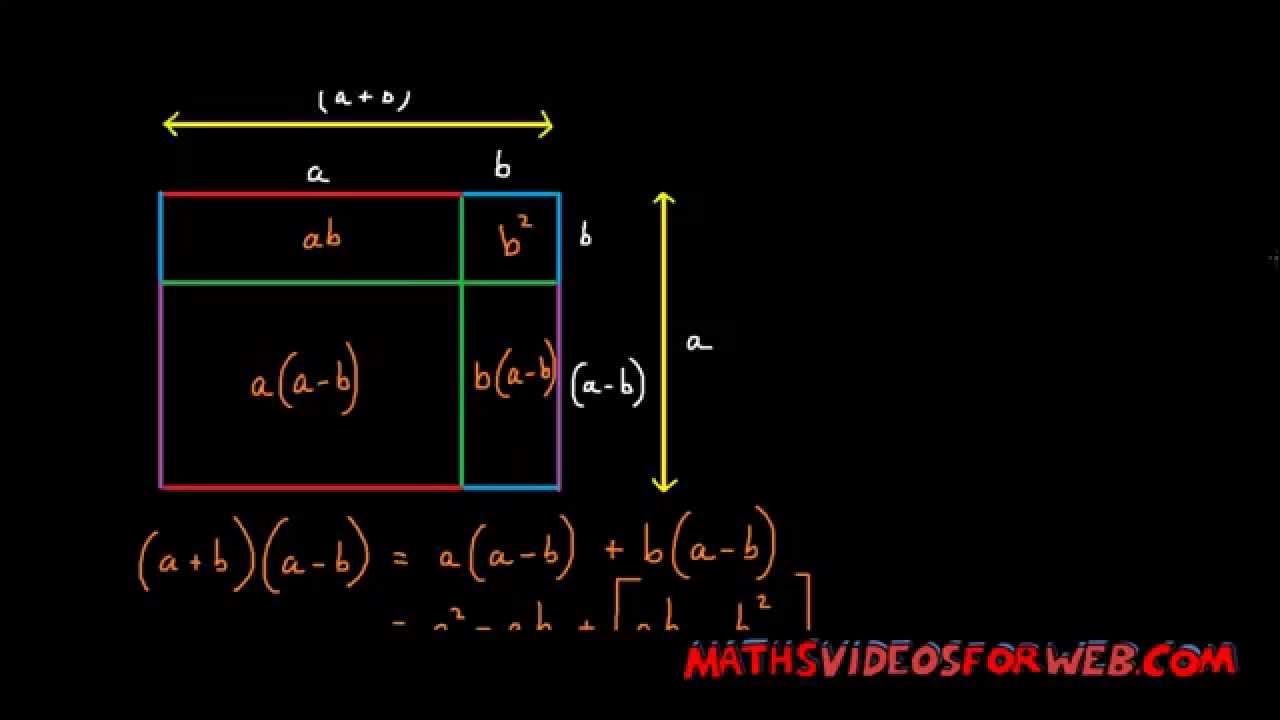
Of: is een lengte a en een oppervlakte S gegeven, construeer dan een lengte x zodat de rechthoek met zijden a + x en x als oppervlakte S heeft: deze opgave laat zich herleiden tot het oplossen van de vergelijking ![]() .
.
Het abstract getal begrip is ongetwijfeld een creatie van de Pythagoreeers; Ze ontwikkelden een vrij hoogstaande theorie van de natuurlijke getallen, waarbij ze ook gebruik maakten van meetkundige figuren. Behandelde onderwerpen uit getallenleer :
- eigenschappen van even en oneven getallen
- theorie van deelbaarheid (priemgetallen)
- theorie van evenredigheden
- kwadraatgetallen, driehoeksgetallen rechthoekige getallen, ruimtelijke getallen
Voor de Pythagoreeers van de oude school waren de natuurlijke getallen de bouwstenen waarmee de hele kosmos kon beschreven worden. Het bestaan van andere dan natuurlijke getallen is voor hen gewoon ondenkbaar. Zij beschouwen breuken dan ook niet als getallen, maar als verhoudingen van twee natuurlijke getallen ( leer van de evenredigheden ). De ontdekking van een getal dat noch een natuurlijk getal is noch een breuk, m.a.w. dat niet rationaal (ratio=rede,verhouding) is, dus irrationaal, betekent dan ook de totale instorting van de kosmologische opbouw van de Pythagoreeers.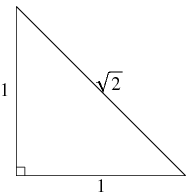
Ze bewijzen dat de schuine zijde en een rechthoekszijde van een rechthoekige driehoek ( met als rechthoekszijden 1 eenheid) onderling onmeetbaar zijn, waarmee bedoeld wordt dat er geen lijnstuk bestaat dat een geheel aantal keren zowel in de schuine als de rechthoekszijde gaat ( = de verhouding van de schuine zijde tot de rechthoekzijde is een irrationaal getal, dat wij voorstellen als ![]() . Alzo doorbreken de Pythagoreeers zelf de begrenzingen van hun getalbegrip.
. Alzo doorbreken de Pythagoreeers zelf de begrenzingen van hun getalbegrip.