
Archimedes leefde in Syracuse van 287 tot. 212 v.C. en verbleef aan het hof van koning Hieron. Bij zijn tijdgenoten verwierf hij grote vermaardheid, niet zozeer voor zijn zuiver wetenschappelijk werk, maar vooral door zijn talrijke technische realisaties van ingenieuze werktuigen en machines( pompen, kranen , katapulten,..).

Als zuiver platonische wiskundige is hij zelf minder gelukkig met zijn materialistische nevenactiviteiten. Tijdens een reis naar Egypte maakt hij kennis met Euclides en vanaf dan onderhoudt hij een vrij drukke wetenschappelijke briefwisseling met andere wiskundigen zoals bvb. Erastosthenes. Meestal deelt hij enkel resultaten mee, daarmee zijn collega’s uitdagend om er zelf een bewijs voor te vinden.

Van zijn uitgebreid oeuvre bleven enkel volgende werken bewaard: Over het evenwicht van vlakke figuren en hun zwaartepunt, de kwadratuur van de parabool, de methode, over de bol en de cilinder, over de conoïden en de sferoïden. over de spiralen, over de drijvende lichamen, de cirkelmeting en de zandrekenaar.

De methode: dit werk werd pas in 1906 bij toeval teruggevonden door de Deense filoloog Heiberg op een palimpsest uit een kloosterbibliotheek. In dit werk leert Archimedes ons dat de strenge deductieve methode , waarvan Aristoteles de formele regels vastlegde en die Euclides in zijn Elementen zo perfect illustreerde, een procédé is dat haast alleen nuttig is om bewijzen van gekende resultaten te leveren.Voor het creatief onderzoekingswerk geeft hij de voorkeur aan zogenaamde mechanische methodes die, omdat ze op fysische inzichten berusten, minder streng maar zoveel vruchtbaarder zijn. Nadat hij langs deze heuristische weg resultaten ontdekt heeft, geeft hij een streng bewijs waarbij hij dikwijls gebruik maakt van Eudoxos’ exhaustiemethode.
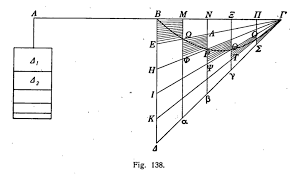
 De voornaamste redenen van de teleurgang van de Griekse meetkunde zijn:
De voornaamste redenen van de teleurgang van de Griekse meetkunde zijn:



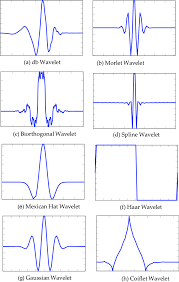
 wavelets
wavelets






