Vaak bestaat een probleem erin aan te tonen dat een bepaalde eigenschap geldt voor elk natuurlijk getal. Als je wilt weten of iets waar is voor alle natuurlijke getallen n (dus voor n = 1, 2, 3, . . .), kun je ze niet allemaal afgaan: daar zou je oneindig lang mee bezig zijn. Inductie is eigenlijk een verzameling van bewijstechnieken die de waarheid van een stelling voor alle elementen van een verzameling aantonen door gebruik te maken van de onderliggende structuur van de verzameling. Om de geldigheid te bewijzen van een uitspraak van de vorm " Voor ieder natuurlijk getal
geldt
", waarbij
staat voor een bewering (propositie) waarin
voorkomt, maakt men vaak gebruik van deze methode. Lees meer hierover in volgend artikel, waar een paar voorbeelden worden uitgewerkt en waar ook een heleboel opgaven staan.
Categorie archieven: Geen categorie
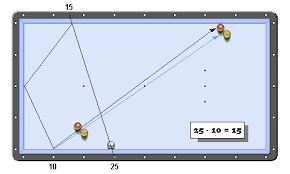
Biljarten onder een hoek van 45°
Als je een biljart tafel hebt van 99 op 101 en je schiet , vanuit de linkerbenedenhoek, een bal weg onder een hoek van 45°, waar komt die dan terecht. In één van de hoeken? En zo ja, na hoeveel botsingen? Lees meer hierover in volgend artikel.
Modulorekenen
De eindige rekenkunde, ook wel modulaire rekenkunde genoemd, wordt beschreven in het boek Disquisitiones Arithmeticae van Gauss, een buitengewoon invloedrijk werk uit 1801, toen de auteur nog maar vierentwintig jaar oud was.
Stel ![]() . Indien
. Indien ![]() en
en ![]() bij deling door
bij deling door ![]() dezelfde rest geven, d.w.z. indien
dezelfde rest geven, d.w.z. indien ![]() voor zekere
voor zekere ![]() , heten
, heten ![]() en
en ![]() congruent modulo
congruent modulo ![]() . We noteren
. We noteren ![]() mod m.Zo is bijvoorbeeld
mod m.Zo is bijvoorbeeld ![]() mod 5,
mod 5, ![]() mod 8 en
mod 8 en ![]() mod 13.
mod 13.
Enkele eigenschappen :
- Als
 mod m en
mod m en  mod m, dan is
mod m, dan is  mod m.
mod m. - Als
 mod m en
mod m en 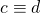 mod m, dan is
mod m, dan is  mod m.
mod m. - Als
 mod m en
mod m en  , dan is
, dan is  mod m.
mod m. - Als
 mod m dan is voor elke
mod m dan is voor elke  :
:  mod m.
mod m. - Als
 mod m en
mod m en 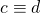 mod m, dan is
mod m, dan is  mod m.
mod m.
Rekenen met congruenties lijkt erg op het rekenen met vergelijkingen. Er is echter een belangrijk verschil: uit ![]() mod m met
mod m met ![]() mod m hoeft niet te volgen dat
mod m hoeft niet te volgen dat ![]() mod m. Zo is
mod m. Zo is ![]() mod 10 maar 12 is niet congruent met 7 modulo 10. In andere gevallen gaat het wel op. De voorwaarde waarop de vereenvoudiging met
mod 10 maar 12 is niet congruent met 7 modulo 10. In andere gevallen gaat het wel op. De voorwaarde waarop de vereenvoudiging met ![]() wel kan, is dat
wel kan, is dat ![]() onderling ondeelbaar is met
onderling ondeelbaar is met ![]() .
.
Dus als ![]() mod m en ggd(c,m) = 1, dan is
mod m en ggd(c,m) = 1, dan is ![]() mod m.
mod m.
Als ggd(c,m) = d, dan volgt uit ![]() mod m dat
mod m dat ![]() mod(
mod( ![]() ).
).
Rekent men modulo ![]() , dan zijn er
, dan zijn er ![]() verschillende soorten getallen, al naar gelang ze verschillende resten geven bij deling door
verschillende soorten getallen, al naar gelang ze verschillende resten geven bij deling door ![]() . De verzameling van alle gehele getallen die eenzelfde rest geven heet een restklasse modulo
. De verzameling van alle gehele getallen die eenzelfde rest geven heet een restklasse modulo ![]() . Er zijn dus precies
. Er zijn dus precies ![]() verschillende restklassen modulo
verschillende restklassen modulo ![]() . De restklasse die een getal
. De restklasse die een getal ![]() bevat, noteert men als
bevat, noteert men als ![]() . Deze notatie is natuurlijk niet eenduidig bepaald, want als
. Deze notatie is natuurlijk niet eenduidig bepaald, want als ![]() mod m, stellen
mod m, stellen ![]() en
en ![]() dezelfde restklasse modulo
dezelfde restklasse modulo ![]() voor en omgekeerd.
voor en omgekeerd.
Werken we modulo 4 dan is ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Men kan in de verzameling restklassen modulo ![]() , genoteerd door
, genoteerd door ![]() , een optelling en een vermenigvuldiging defini\”eren via
, een optelling en een vermenigvuldiging defini\”eren via ![]() en
en ![]() . Deze rekenregels lijken erg op de regels van optelling en vermenigvuldiging van gehele getallen.
. Deze rekenregels lijken erg op de regels van optelling en vermenigvuldiging van gehele getallen.
Eigenschappen :

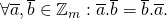
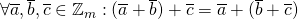 .
. .
. .
.
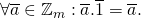
- Er is een unieke restklasse
 met
met  , namelijk
, namelijk  .
.
Veronderstel dat we de rest willen bepalen van ![]() bij deling door 7. Omdat
bij deling door 7. Omdat ![]() mod 7 en
mod 7 en ![]() mod 7, moet
mod 7, moet ![]() mod 7
mod 7 ![]() mod 7
mod 7 ![]() mod 7. Dus de rest bij deling van
mod 7. Dus de rest bij deling van ![]() door 7 is 2. We moeten daarvoor het product niet uitrekenen.
door 7 is 2. We moeten daarvoor het product niet uitrekenen.
Hoofdstelling van de rekenkunde
Elk samengesteld getal kan geschreven worden als het product van kleinere factoren. Als minstens 1 van beide samengesteld is , kan men die ook weer schrijven als product van kleinere factoren. Zo kan men doorgaan tot er slechts priemgetallen als factoren overblijven. men kan een samengesteld getal in het algemeen op verschillende manieren via een aantal tussenstappen in priemgetallen ontbinden. Het uiteindelijk resultaat, de ontbinding in priemfactoren, is steeds hetzelfde. Dit resultaat staat bekend als de hoofdstelling van de rekenkunde:
![]()
Deze eigenschap is in andere getalsysytemen niet noodzakelijk waar. Beschouw de verzameling van de even getallen ![]() . Sommige ervan kan men schrijven als het product van even factoren, bijvoorbeeld
. Sommige ervan kan men schrijven als het product van even factoren, bijvoorbeeld ![]() . Bij andere is dat niet mogelijk. We noemen even getallen die niet het product zijn van even factoren even-priemgetallen. Een even getal is te schrijven als product van even-priemgetallen, maar zo een ontbinding hoeft niet eenduidig te zijn. Zo is
. Bij andere is dat niet mogelijk. We noemen even getallen die niet het product zijn van even factoren even-priemgetallen. Een even getal is te schrijven als product van even-priemgetallen, maar zo een ontbinding hoeft niet eenduidig te zijn. Zo is ![]()
Als een getal ontbonden is in priemfactoren, dan kan men het aantal delers bepalen. Stel dat ![]() dan heeft
dan heeft ![]() juist
juist ![]() delers.
delers.
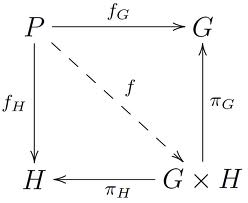
Groepsconstructies
In deze tekst bespreken we hoe we van twee groepen een nieuwe groep kunnen maken of hoe we een groep kunnen ‘ontbinden’ als een product van kleinere groepen.