We geven eerst de definitie : ![]() en
en ![]() . Uit deze definitie leid je onmiddellijk af dat
. Uit deze definitie leid je onmiddellijk af dat ![]() en
en ![]() .
.
Andere eigenschappen:

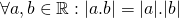


 (driehoeksongelijkheid)
(driehoeksongelijkheid)

De grafiek van de functie ![]() wordt gegeven door:
wordt gegeven door:

Een man beschikt over een klein roeibootje. Hij moet een wolf, een schaap en
een kool naar de andere oever overbrengen. In het bootje is maar plaats voor
de man en ofwel de wolf, ofwel het schaap, ofwel de kool. Hij mag echter de
wolf en het schaap nooit alleen laten (je kan wel raden wat er dan gebeurt)
en ook het schaap mag hij niet alleen met de kool achterlaten. Hoe legt hij
het aan boord?
Over de oplossing en aanverwante problemen kan je meer lezen in volgend artikel.
Sommige stellingen zijn zo eenvoudig en elegant dat je jezelf kan afvragen: Waarom ben ik daar niet zelf op gekomen? Dit geldt onder andere voor de volgende stelling die vernoemd wordt naar zijn ontdekker: de Oostenrijkse wiskundige Georg Alexander Pick, geboren in 1859 in Wenen en overleden in 1942 in het concentratiekamp Theresienstadt.
Het gaat over de oppervlakte van een roosterveelhoek, dit wil zeggen een veelhoek waarvan de hoekpunten op de punten van een regelmatig vierkant rooster liggen. Noteer met ![]() het aantal roosterpunten op de rand van de veelhoek V en met
het aantal roosterpunten op de rand van de veelhoek V en met ![]() het aantal roosterpunten in het inwendige van V.
het aantal roosterpunten in het inwendige van V.
![]()
Voor deze veelhoek is de oppervlakte dus ![]() oppervlakte eenheden.
oppervlakte eenheden.
Door onze wiskundige ervaring beperken we ons soms tot die oplossingsmethoden die in het verleden steeds gewerkt hebben. Daardoor zie je soms een eenvoudige uitkomst over het hoofd. Een belangrijke heuristiek is bijgevolg: het probleem op een andere manier bekijken. We noemen dit blikwissel.
We doen alsof we de oplossing hebben en werken zo terug tot we terechtkomen bij een situatie die we wel meester zijn. We proberen een omgekeerde redenering op te zetten door van achter naar voor werken. We leven ons in in de personen, dieren, zaken die in de vraag voorkomen en bekijken het probleem eens vanuit hun standpunt. We kijken naar andere dingen, die niet rechtstreeks gevraagd zijn. We vragen ons af wat de voorlaatste stap van de oplossing zou kunnen zijn.
Bekijken we volgend voorbeeld:
Je beschikt over twee emmers, één van 9 liter en een van 4 liter. Hoe kan je hiermee precies 6 liter water uit een waterput afmeten?
We vragen ons af wat de voorlaatste stap van de oplossing zou kunnen zijn. Om 6 liter in de emmer van 9 liter over te houden, willen we die helemaal vullen en er 3 liter uit wegnemen. Dit lukt als we in de kleine emmer 1 liter water hebben staan. Hoe kunnen we nu 1 liter maken met deze twee emmers? Nu is ![]() . Onze strategie is dus:
. Onze strategie is dus: