Veronderstel nu even dat Peter wel de constante c kent waarmee hij kan ontsnappen, maar dat hij de startpositie ![]() niet kent. Dit leidt ons naar de definitie van de Juliaverzamelingen, genoemd naar de wiskundige Gaston Julia ( 1893-1978): voor een gegeven complex getal c, zullen sommige beginpunten
niet kent. Dit leidt ons naar de definitie van de Juliaverzamelingen, genoemd naar de wiskundige Gaston Julia ( 1893-1978): voor een gegeven complex getal c, zullen sommige beginpunten ![]() een divergerende rij
een divergerende rij ![]() genereren, terwijl andere startpunten niet-divergerende rijen voortbrengen. De Julia verzameling is de grens die de divergerende startpunten scheidt van de niet-divergerende startpunten.
genereren, terwijl andere startpunten niet-divergerende rijen voortbrengen. De Julia verzameling is de grens die de divergerende startpunten scheidt van de niet-divergerende startpunten.
Neem bijvoorbeeld ![]() . Punten die binnen de eenheidscirkel liggen worden aangetrokken door de oorsprong. Punten erbuiten zullen verder en verder van de oorsprong bewegen. de Julia verzameling voor
. Punten die binnen de eenheidscirkel liggen worden aangetrokken door de oorsprong. Punten erbuiten zullen verder en verder van de oorsprong bewegen. de Julia verzameling voor ![]() is dus de eenheidscirkel.
is dus de eenheidscirkel.
Enkele mooie Juliaverzamelingen zijn:
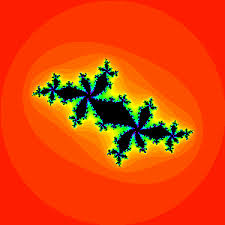
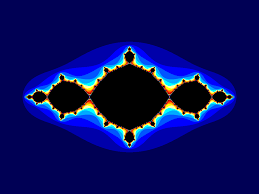
We kunnen ons de vraag stellen wanneer deze Juliaverzamelingen een samenhangende figuur vormen. Het waren de wiskundigen John Hubbard en Adrien Douady ( zie foto ) die vonden dat dit gebeurde voor de c-waarden die tot de Mandelbrotverzameling behoorden.