Tussen 3000 en 2000 v.C ontstond op de Cycladen een pre-Griekse beschaving. Deze eilandengroep in de Egeïsche zee, met als grootste eilanden Paros,Delos,Minos en Santorini dankt zijn naam aan de rangschikking in een cirkel.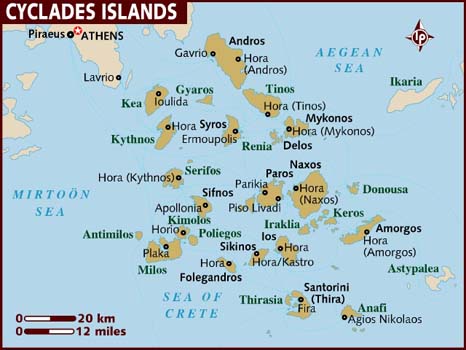
De eilandengroep ligt op een strategische plaats tussen Europa en Azië. Al zeer vroeg kozen de eilandbewoners het ruime sop en konden zo vreemde cultuurinvloeden overnemen.
De Cycladische maatschappij was welvarend. De bewoners waren zeelui die handel dreven in het oostelijke Middellandse Zeegebied. Maar het waren niet alleen vissers en handelslui, maar ook boeren, veehouders en jagers. Ze werkten op het platteland, ze hadden eigen wijn, olijfolie, groenten, ze cultiveerden hun grond en brachten hun leven vredelievend door. De inwoners van de Cycladen waren artistiek, het bewijs hiervan zijn de vele vazen, juwelen en andere voorwerpen die uit die periode teruggevonden zijn
De belangrijkste werken waren echter kleine in wit marmer, modern ogende beeldjes (idolen), zonder gelaat en alleen een neus. De beeldjes zijn herleid tot de geometrische grondvormen. Opvallend was dat de beeldjes meestal vrouwen,nimfen of Godinnen voorstelden. De mannelijke beelden waren vooral beelden van jagers, van mannen die dansten of van mannen die een muziekinstrument bespeelden. Veel van de voorwerpen die ze maakten, verkochten ze op Kreta, daar woonden de Minoërs. Doordat ze in aanraking kwamen met de Minoïsche beschaving, brachten ze de kunst uit Kreta ook naar de Cycladen. 
Er kwam een einde aan hun beschaving toen de Minoërs (Kreta) binnen vielen en toen rond 1600 v.C. een vulkaanuitbarsting een groot deel van Santorini vernielde