Categorie archieven: Geen categorie

Bewijzen met verhaaltjes

Geplaatst op door

Deze bewijstechniek bestaat er in ‘een verhaaltje te vertellen. 

Stel ik wil volgende formule “bewijzen”:  voor n\geq p\geq 2

    \[p(p-1)\binom{n}{p}=n(n-1)\binom{n-2}{p-2}\]

Je zou natuurlijk, gebruikmakend van de definitie van de binomiaalgetallen, beide leden kunnen uitrekenen, en vaststellen dat beide resultaten hetzelfde zijn. Maar proberen we dit eens anders in te kleden. Je hebt binnen een politieke partij n kaderleden, waaruit je een dagelijks bestuur van p personen moet kiezen, met hierin een voorzitter en een ondervoorzitter. Dit kan je doen op twee manieren :

  • Kies eerst p personen. Dit kan op 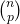\binom{n}{p}. Kies hier uit een voorzitter: p mogelijkheden. Kies dan een ondervoorzitter: p – 1 mogelijkheden. Samen geeft dit dus, als aantal mogelijkheden:

        \[p(p-1)\binom{n}{p}\]

  • Maar je kan eerst een voorzitter kiezen uit de n kaderleden. Dit kan je op n mogelijkheden. Kies vervolgens een ondervoorzitter: n – 1 mogelijkheden. Kies tenslotte nog p-2 ander personen om je dagelijks bestuur te vervolledigen. dit kan op \binom{n-2}{p-2} manieren. Zo krijg je in het totaal als mogelijkheden:

        \[n(n-1)\binom{n-2}{p-2}\]

Hiermee is de gevraagde formule bewezen!

Het postulaat van Bertrand

Geplaatst op door

Het postulaat van Bertrand is een bekende stelling in de getaltheorie die stelt dat er voor elk natuurlijk getal  n>1 altijd minstens één priemgetal p bestaat tussen n en 2n. Men kan zelfs bewijzen dat voor n > 5 er tussen n en 2n ten minste twee priemgetallen liggen. Neem bijvoorbeeld n=127, dan merken we  tussen 127 en 254 de priemgetallen 139 en 163 op. 

Het postulaat werd in 1845 geformuleerd door de Franse wiskundige Joseph Bertrand (1822-1900) op basis van empirische waarnemingen. Hij testte de bewering voor alle getallen tot 3 miljoen en vond geen tegenvoorbeeld. Een volledig formeel bewijs werd echter pas in 1852 geleverd door de Russische wiskundige Pafnoeti Tsjebysjev, waardoor de stelling ook wel bekendstaat als de stelling van Tsjebysjev.

Later werden er eenvoudigere bewijzen gevonden, waaronder een elegant bewijs met behulp van de priemgetalstelling en methoden van Ramanujan en Erdős.

Het postulaat van Bertrand is belangrijk in de getaltheorie omdat het inzicht geeft in de verdeling van priemgetallen. Het leidt tot enkele nuttige resultaten, zoals:

  • Een snellere benadering van priemgetallen: Dit postulaat garandeert bijvoorbeeld dat er altijd een priemgetal is tussen n en 2n, wat handig is bij algoritmes die priemgetallen genereren.
  • Het product van de k eerste priemgetallen is kleiner dan 2^k.
  • In de ontbinding in priemfactoren van n! staat er minstens 1 priemgetal met exponent 1.

In het algemeen blijft het postulaat een belangrijk voorbeeld van hoe priemgetallen over de natuurlijke getallen verdeeld zijn en inspireerde het verder onderzoek naar priemgetaldistributies.

Nog 5 haiku’s

Geplaatst op door

Nu het verbeteren achter de rug is , de laatste haiku’s van het jaar , in volgorde  gemaakt door Toon Wielemans, Victor Peuters, Iben Eembeeck, Tristan Boschman en Mateja Marcos/

breuk van sin op cos

tussen nul en oneindig

gelijk aan rico

 

algebra fluistert

onbekende letter staat

de oplossing wacht

snijdende rechten

komen samen in één punt

dan gewoon verder

getal na getal

verschillen en producten

oplossing verschijnt

even spiegelt mooi

oneven doet dat door nul

symmetrie doet mee

Nootje 52

Geplaatst op door

Een bol is ingeschreven in een afgeknotte kegel en het volume van de bol is de helft van het volume van de afgeknotte kegel. Bereken de verhouding van de stralen van boven en ondervlak van die afgeknotte kegel.

Antwoord